Предмет: Алгебра,
автор: davelombardo
допоможіть будь ласка
Приложения:
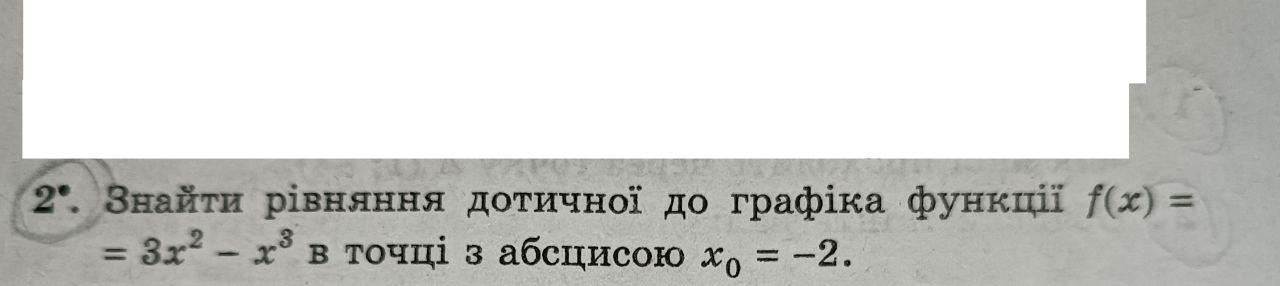
Ответы
Автор ответа:
1
Ответ:
Для нахождения касательной к графику функции \(f(x) = 3x² - x³\) в точке с абсциссой \(x_0 = -2\) мы используем саму функцию при \(x = -2\). Теперь подставим \(x = -2\) в функцию:
\[f(-2) = 3 * (-2)² - (-2)³\]
\[f(-2) = 3 * 4 - (-8)\]
\[f(-2) = 12 + 8\]
\[f(-2) = 20\]
Таким образом, мы получили точку (-2, 20) на графике функции. Чтобы найти уравнение касательной, вычислим производную функции \(f(x) = 3x² - x³\):
\[f'(x) = 6x - 3x²\]
Подставим \(x = -2\) в производную функции, чтобы найти значение тангенса угла наклона касательной:
\[f'(-2) = 6 * (-2) - 3 * (-2)²\]
\[f'(-2) = -12 - 12\]
\[f'(-2) = -24\]
Таким образом, тангенс угла наклона касательной в точке с \(x = -2\) равен -24. Уравнение касательной будет: \(y - 20 = -24(x + 2)\).
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: romancenkonatalia35
Предмет: Українська мова,
автор: krestee
Предмет: Русский язык,
автор: dmakash1792
Предмет: Русский язык,
автор: Microsof593
Предмет: Алгебра,
автор: anika13032006