Предмет: Геометрия,
автор: dlolz404ons
Довжина кола, описаного навколо правильного чотирикутника, дорівнює 20П(пі) см. Знайдіть периметр чотирикутника
Приложения:

zmeura1204:
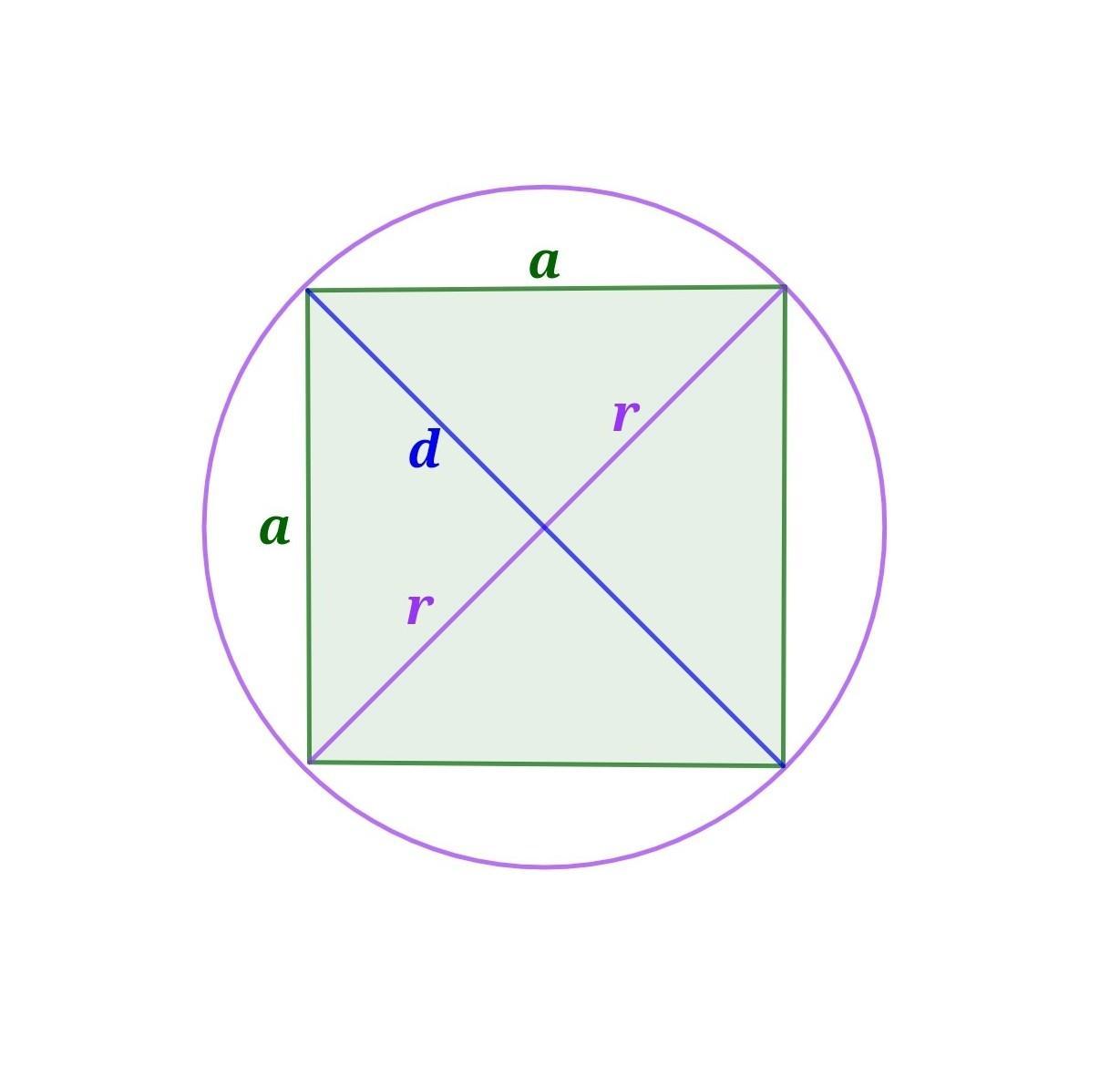
С=πD; → D=C/π=20π/π=20 діаметр і діагональ квадрата. а=D/√2=20/√2=10√2 сторона квадрата. Р=4а=40√2
на листке
Самі.
☆☆☆☆☆
Ответы
Автор ответа:
3
Ответ:
Периметр чотирикутника дорівнює 40√2 см
Объяснение:
УМОВА: Довжина кола, описаного навколо правильного чотирикутника, дорівнює 20π см. Знайдіть периметр чотирикутника.
РОЗВ'ЯЗАННЯ:
1.
Довжина описаного кола L визначається формулою:
де r - радіус описаного кола.
За умовою L = 20π (см).
Знайдемо радіус описаного кола:
Отже, радіус описаного кола становить 10 см.
2.
У правильному чотирикутнику (квадраті) діагональ d є діаметром описаного кола, тобто:
d = 2 • 10 = 20(см)
3.
У квадраті сторона а і діагональ d пов'язані формулою:
Знайдемо сторону квадрата а:
(см)
4.
Периметр Р квадрата дорівнює сумі його чотирьох сторін:
P=4•10√2=40√2 (см)
ВІДПОВІДЬ: 40√2 см
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: olga47pwpwpwwow
Предмет: Химия,
автор: denni4444like
Предмет: Литература,
автор: Wexexortquas
Предмет: Геометрия,
автор: vadim6468
Предмет: Химия,
автор: dimaw0308209