Предмет: Геометрия,
автор: yeatt
В трапецию с острыми углами альфа и бета вписана окружность радиусом R. Найдите периметр и площадь этой трапеции. (с рисунком пожалуйста)
Ответы
Автор ответа:
1
Ответ:
Периметр трапеции равен 4R(sinα+sinβ)/sinα*sinβ;
Площадь трапеции равна 2R²(sinα+sinβ)/sinα*sinβ;
Объяснение:
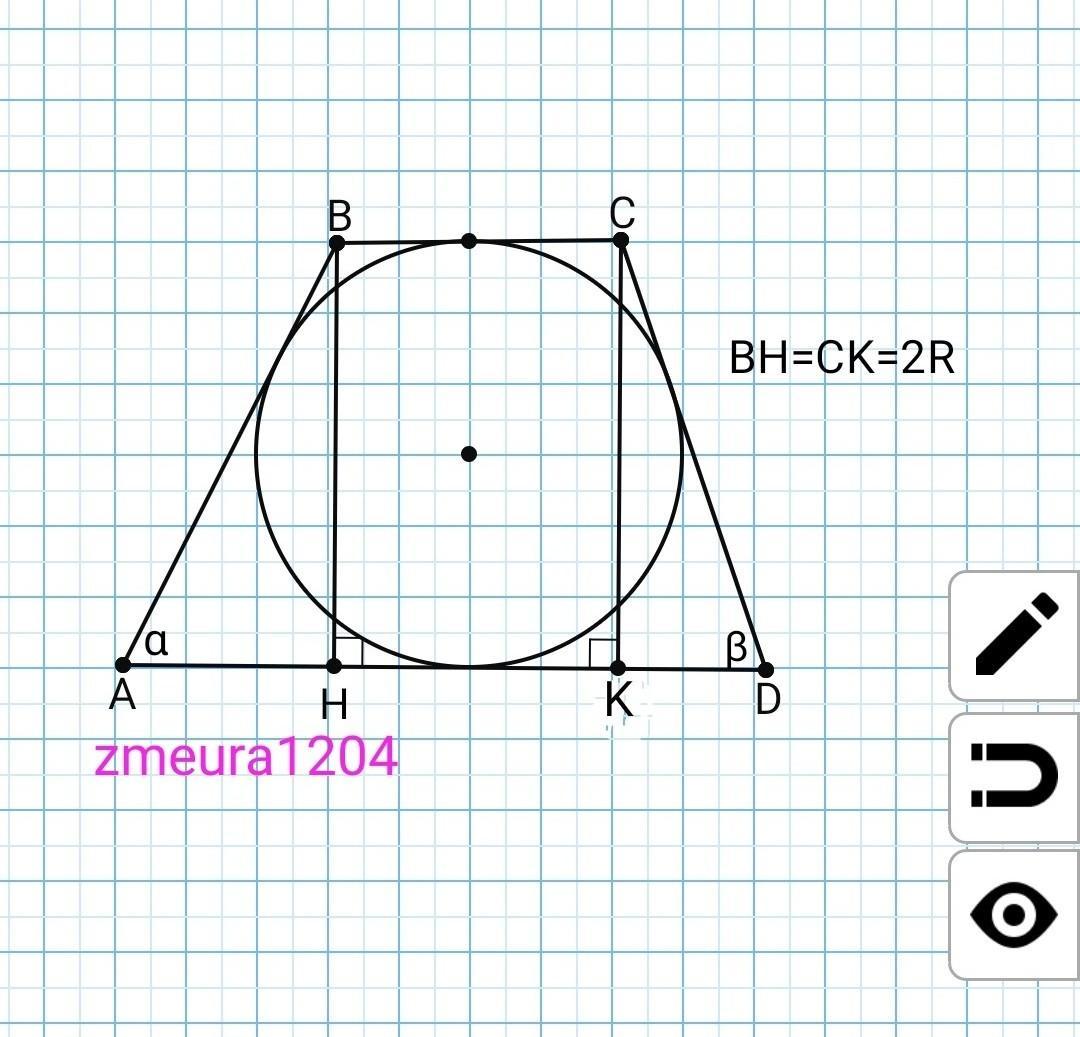
∆BAH- прямоугольный треугольник.
sin∠A=BH/AB;
AB=BH/sin∠A=2R/sinα;
∆CKD- прямоугольный треугольник
sin∠D=CK/CD;
CD=CK/sin∠D=2R/sinβ;
Если в трапецию можно вписать окружность, то сумма боковых сторон равна сумме оснований.
AD+BC=AB+CD.
AB+CD=2R/sinα+2R/sinβ=
=(2Rsinβ+2Rsinα)/sinα*sinβ.
P=2(AB+CD)=2(2Rsinβ+2Rsinα)/sinα*sinβ=
4R(sinβ+sinα)/sinα*cosβ.
S=BH(AD+BC)/2=(2R/2)*(2Rsinβ+2Rsinα)/sinα*sinβ=
=2R²(sinα+sinβ)/sinα*sinβ
Приложения:
yeatt:
СПАСИБО ВАМ ОГРОМНОЕ!!
Похожие вопросы
Предмет: Английский язык,
автор: angelinametlina7
Предмет: Математика,
автор: timofeykoleso14322
Предмет: Другие предметы,
автор: zhantleyev
Предмет: Математика,
автор: DiSunPlay
Предмет: Информатика,
автор: Takotopmost