Предмет: Математика,
автор: romanovaarina108
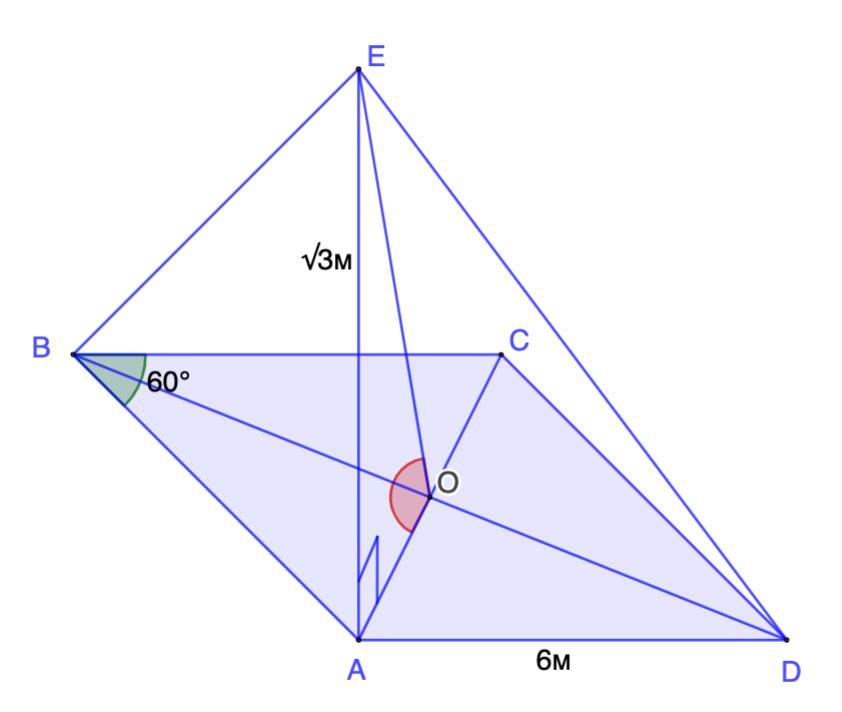
Через вершину А ромба ABCD со стороной равной 6м и острым углом В равным 60° провели перпендикуляр AE = корень 3 м.
Найдите угол наклона плоскости DBE к плоскости треугольника ABC.
amelelilineli:
Ответ нашли?
Ответы
Автор ответа:
1
Ответ:
Угол наклона плоскости DBE к плоскости треугольника ABC равен 30°.
Пошаговое объяснение:
Через вершину А ромба ABCD со стороной равной 6м и острым углом В равным 60° провели перпендикуляр AE = √3 м.
Найдите угол наклона плоскости DBE к плоскости треугольника ABC.
Дано: ABCD - ромб;
АВ = 6 м;
ЕА ⊥ (АВС); ЕА = √3 м;
∠В = 60°.
Найти: угол наклона (DBE) к (АВС)
Решение:
ABCD - ромб;
- Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
⇒ АС ⊥ BD; АС ⊂ (АВС)
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒ EO ⊥ BD; ЕО ⊂ (DBE)
- Угол между двумя плоскостями - угол между перпендикулярами, проведенными в каждой из плоскостей из точки, принадлежащей линии пересечения плоскостей .
⇒ ∠ЕОА - искомый угол.
Рассмотрим ΔАВС - равнобедренный (АВ = ВС)
∠В = 60°
- Если в равнобедренном треугольнике есть угол 60°, то он равносторонний.
⇒ АВ = ВС = АС = 6 м.
АО = АС : 2 = 6 : 2 = 3 (м)
Рассмотрим ΔАЕО - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Физика,
автор: shshshkss
Предмет: Химия,
автор: mariamalashenko1907
Предмет: Алгебра,
автор: kostakuceravij041
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: alibobo1999