Предмет: Алгебра,
автор: hadsonhornet0087
2. Решите уравнение с помощью универсальной тригонометрической подстановки:
Приложения:
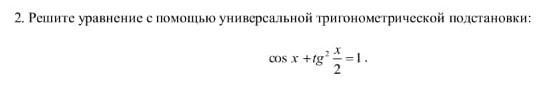
Ответы
Автор ответа:
2
Ответ:
Универсальная тригонометрическая подстановка :
Решить уравнение .
Вернёмся к старой переменной .
Серии решений b) и с) можно объединить и записать :
Ответ: .
Приложения:

Похожие вопросы
Предмет: Математика,
автор: GoshaTurboTech5
Предмет: Химия,
автор: vanyafomenko195
Предмет: Алгебра,
автор: oioioi098
Предмет: Химия,
автор: superzeldabros64
Предмет: География,
автор: victorianykolaychuk