Question

СРОЧНО ПОМОГИТЕ МНЕ ОЧЕНЬ НАДА ППЖПЖПЖ ДАМ 100 БАЛЛОВ

Answer 1

Ответ:

Пошаговое объяснение:

1.

$158*(\frac{12-\frac{12}{7}-\frac{12}{289}-\frac{12}{85}}{4-\frac{4}{7}-\frac{4}{289}-\frac{4}{85}}:\frac{5-\frac{5}{13}-\frac{5}{169}-\frac{5}{91}}{6-\frac{6}{13}-\frac{6}{169}-\frac{6}{91}})*\frac{505505505}{711711711}$

Будем проводить вычисления по порядку:

$\textbf{1)}\ \frac{12-\frac{12}{7}-\frac{12}{289}-\frac{12}{85}}{4-\frac{4}{7}-\frac{4}{289}-\frac{4}{85}}=\frac{12(1-\frac{1}{7}-\frac{1}{289}-\frac{1}{85})}{4(1-\frac{1}{7}-\frac{1}{289}-\frac{1}{85})} =\frac{12}{4} =3\\\\\textbf{2)}\ \frac{5+\frac{5}{13}+\frac{5}{169}-\frac{5}{91}}{6+\frac{6}{13}+\frac{6}{169}-\frac{6}{91}}=\frac{5(1+\frac{1}{13}+\frac{1}{169}-\frac{1}{91})}{6(1+\frac{1}{13}+\frac{1}{169}-\frac{1}{91})} =\frac{5}{6}\\\\\textbf{3)}\ 3\ :\ \frac{5}{6}=3*\frac{6}{5} =3.6$

$\textbf{4)}\ 158*3.6=568.8\\\\\textbf{5)}\ \frac{505505505}{711711711} =\frac{505000000+505000+505}{711000000+711000+711} =\frac{505(1000000+1000+1)}{711(1000000+1000+1)} =\frac{505}{711} \\\\\textbf{6)}\ 568.8*\frac{505}{711}=\fbox{404}$

2.

Двузначные числа, которые начинаются на 4:

40, 41, 42, ..., 49

Двузначные числа, которые заканчиваются 4:

14, 24, 34, ..., 94

Посчитаем сумму всех этих чисел как сумму n-членов арифм. прогрессии:

• $S_n=\frac{(a_n+a_1)}{2}*n$

Для первого ряда:

$a_1=40\\a_n=49\\n=10\\S_{10}=\frac{40+49}{2} *10=445$

Для второго ряда:

$a_1=14\\a_n=94\\n=9\\S_n=\frac{14+94}{2}*9= 486$

Сложим оба результата, а так же вычтем из него один раз число 44, поскольку мы посчитали его два раза (для первой прогрессии и для второй):

$S=445+486-44=\fbox{887}$

3.

• НОД двух некоторых чисел a и b - это такое наибольшее число, на которое можно разделить без остатка как a, так и b.
• Из этого можно вывести следующее представление a и b: a = НОД(a, b) * k, b = НОД(a, b) * l, где k и l - взаимно простые числа, то есть числа, которые не имеют общих делителей кроме ±1.

Перепишем нашу сумму в следующем виде:

$m+n=80\\6k + 6l = 80\\6(k+l)=80$

Заметим, что левая часть у нас делится на 6, но тогда и правая часть должна делиться на 6.

80 не делится нацело на 6, из чего можно сделать вывод, что не существует таких натуральных чисел m и n, для которых выполнялось бы наше условие.

4.

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\dots+\frac{1}{99}-\frac{1}{100}=\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+\dots+\frac{1}{99}+\frac{1}{100}$

Заметим, что при дробях с четными знаменателями у нас стоит знак -, а при дробях с нечетными знаменателями у нас стоит знак +.

Перенесем правую часть с противоположным знаком и посмотрим что получится:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\dots+\frac{1}{99}-\frac{1}{100}-\frac{1}{51}-\frac{1}{52}-\frac{1}{53}-\dots-\frac{1}{99}-\frac{1}{100}=0$

Учитывая, что дроби с нечетными знаменателями - положительны, то при переносе левой части в правую у нас сокращаются все дроби с нечетными знаменателями большие и равные 51.

В свою очередь, дроби с четными показателями большие и равные 52 - складываются.

В итоге у нас получается:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{2}{52}-\frac{2}{54}-\frac{2}{56} -\dots-\frac{2}{100}=0$

При сокращении дробей правой части у нас получается:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{1}{26}-\frac{1}{27}-\frac{1}{28} -\dots-\frac{1}{50}=0$

Опять же дроби с нечетными показателями большие и равные 27 - сокращаются, а дроби с четными показателями большие и равные 26 - складываются. Получается:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{2}{26}-\frac{2}{28} -\frac{2}{30} -\dots-\frac{2}{50}=0$

Опять сокращаем правую часть и получаем:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{1}{13}-\frac{1}{14} -\frac{1}{15} -\dots-\frac{1}{25}=0$

Дроби с нечетными знаменателями большие 13 - исчезают, с четными знаменателями большие 14 - складываются:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{2}{14} -\frac{2}{16} -\dots-\frac{2}{24}=0$

Проделываем этот трюк снова и снова, в конечном итоге получая:

$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{1}{7} -\frac{1}{8} -\dots-\frac{1}{12}=0\\\\1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{2}{8}- \frac{2}{10}-\frac{2}{12}=0\\\\1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\dots-\frac{1}{4}- \frac{1}{5}-\frac{1}{6}=0\\\\1-\frac{1}{2}+\frac{1}{3}-\frac{2}{4}-\frac{2}{6}=0\\\\1-\frac{1}{2}+\frac{1}{3}-\frac{1}{2}-\frac{1}{3}=0\\\\1-\frac{2}{2}=0\\\\ 1-1=0\\\\0=0$

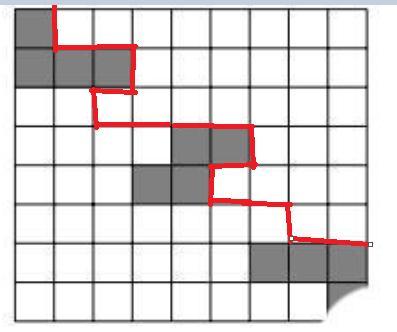
5.

Прикрепил рисунок. Перемещаем верхнюю часть на две клетки вправо и на 2 клетки вниз. Далее стыкуем ее и получаем прямоугольник со сторонами 6 и 10.