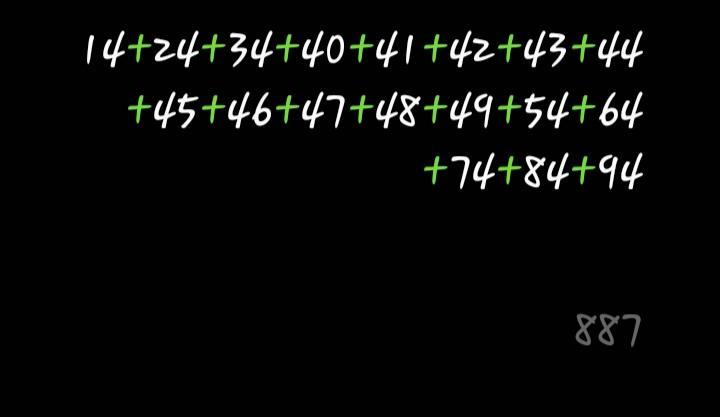1. Знайдіть суму всіх двоцифрових чисел, які починаються на 4 або закінчу- ються на 4.
Ответы
Ответ:
Щоб знайти суму всіх двоцифрових чисел, які починаються на 4 або закінчуються на 4, можемо розглянути всі можливі варіанти.
Двоцифрові числа, що починаються на 4, мають вигляд 40, 41, ..., 49. Сума таких чисел може бути знайдена за допомогою формули арифметичної прогресії:
\[ S_1 = \frac{n_1(a_1 + a_n)}{2} \]
де \( n_1 \) - кількість членів, \( a_1 \) - перший член, \( a_n \) - останній член.
Аналогічно, для чисел, що закінчуються на 4, маємо 4, 14, 24, ..., 94.
\[ S_2 = \frac{n_2(a_2 + a_m)}{2} \]
Знайдемо суми для обох випадків і додаймо їх:
\[ S = S_1 + S_2 \]
Тут \( n_1 = n_2 = 10 \) (10 чисел у кожній послідовності), \( a_1 = 40 \), \( a_n = 49 \) для першої послідовності, \( a_2 = 4 \), \( a_m = 94 \) для другої.
Підставимо значення та знайдемо суму.
Ответ: 887
Объяснение: 14+24+34+40+41+42+43+44+45+46+47+48+49+54+64+74+84+94=887