Предмет: Алгебра,
автор: arikknoroz3
Даю 90б допоможіть будь ласка
Побудувати графік функції y =
-x^2 + 6x - 5 і визначити її:
1) найменше значення;
2) проміжки, у яких f(x)>0 f(x)<0
3) корені рівняння f(x) = -3
Ответы
Автор ответа:
0
Ответ:
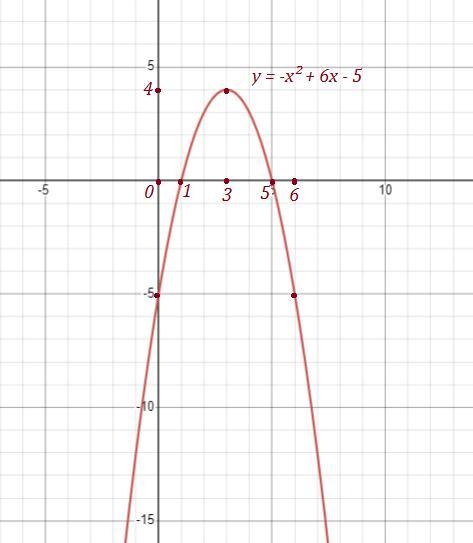
Начертим график параболы у = -х² + 6х - 5 .
Ветви параболы направлены вниз, так как а = -1 <0 .
Координаты вершины : ( 3 ; 4 ) .
Проходит через точки ( 0 ; -5 ) , ( 6 ; -5 ) .
Точки пересечения с осью ОХ : -x² + 6x - 5 = 0 ⇒ x² -6x + 5 =0 ,
x = 1 , x = 5 (теорема Виета) .
1) Наибольшее значение функции : у = 4 .
2) y > 0 при x ∈ ( 1 ; 5 )
y < 0 при x ∈ (-∞ ; 1 ) ∪ ( 5 ; +∞)
3) y = -3 ⇒ -x² + 6x - 5 = -3 , x² - 6x + 2 =0 , D = b² -4ac = 36 -8 =28
x₁ = (6 - √28)/2 = 3 -√7 , x₂ = 3 + √7 .
Приложения:
Похожие вопросы