Даю 75 баллов за одно задание (50б за ответ + 25б за лучший), это очень просто для тех кто знает, нужно сегодня!!

Ответы
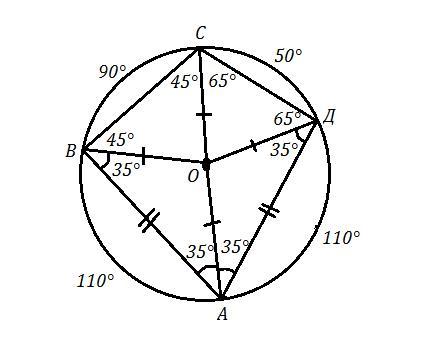
Ответ: 110° , 90° , 50° , 110° .
АВСД - четырёхугольник . Так как он вписан в окружность , то сумма противоположных его углов равна 180° .
Значит углы в 70° и 110° лежат напротив друг друга и углы в 80° и 100° тоже лежат напротив друг друга .
Пусть ∠А =70° , ∠С = 110° , ∠В = 80° , ∠Д = 100° .
По условию стороны, которые образуют наименьший угол , равны . Тогда АВ = АД .
Соединим центр вписанной окружности, точку О, с вершинами А , В , С и Д .
Рассмотрим Δ АОВ . ОА = ОВ как радиусы ⇒ Δ АОВ - равнобедренный и ∠ОАВ = ∠ОВА .
Рассмотрим Δ АОД . ОА = ОД как радиусы ⇒ Δ АОД - равнобедренный и ∠ОАД = ∠ОДА .
Причём по условию АВ = АД , значит Δ АОВ = Δ АОД по трём сторонам ⇒ ∠ОАВ = ∠ОАД , но ∠А = ∠ОАВ + ∠ОАД = 70° ⇒
∠ОАВ = ∠ОАД = 70° : 2 = 35° .
∠ОВА = ∠ОДА = ∠ОАВ = ∠ОАД = 35° .
∠В = ∠ОВА + ∠ОВС = 80° ⇒ 80° = 35° + ∠ОВС ,
∠ОВС = 80° - 35° = 45°
Δ ОВС - равнобедренный , ОВ = ОС как радиусы ⇒
∠ОСВ = ∠ОВС = 45°
∠С = ∠ОВС + ∠ОСВ ⇒ 110° = 45° + ∠ОСВ ,
∠ОСВ = 110° - 45° = 65°
Δ ОСД - равнобедренный , ОС = ОД как радиусы ⇒
∠ОДС = ∠ОСД = 65° ( или ∠ОДС = ∠Д - 35° = 100° - 35° = 65° )
Теперь найдём градусные меры дуг, на которые вершины А , В , С , Д делят окружность .
Центральный ∠АОВ опирается на дугу АВ , их градусные меры равны : ∠АОВ = 180° - 35° - 35° = 110° ( из Δ АОВ ) .
Центральный ∠ВОС опирается на дугу ВС , их градусные меры равны : ∠ВОС = 180° - 45° - 45° = 90° ( из Δ ВОС ) .
Центральный ∠СОД опирается на дугу СД , их градусные меры равны : ∠СОД = 180° - 65° - 65° = 50° ( из Δ СОД ) .
Центральный ∠АОД опирается на дугу АД , их градусные меры равны : ∠АОД = 180° - 35° - 35° = 110° ( из Δ АОД ) .
Проверка . 110° + 90° + 50° + 110° = 360°