Предмет: Алгебра,
автор: solixaa888
Решите пожалуйста четвертый и седьмой пример
Приложения:
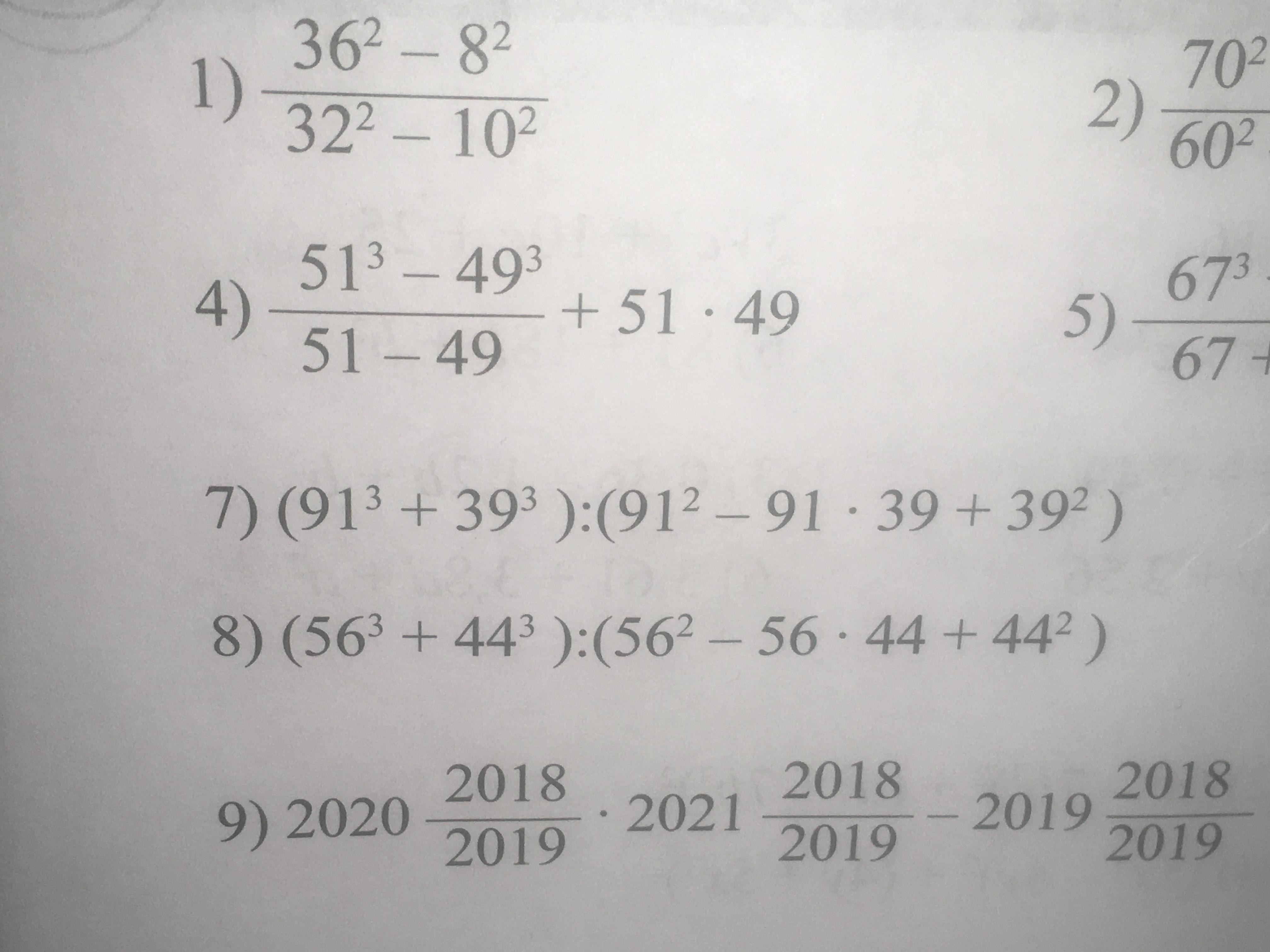
Ответы
Автор ответа:
1
Решение
Преобразуем числитель дроби по формуле разности кубов двух выражений:
Сократим дробь:
Свернем полученное выражение по формуле квадрата суммы двух выражений:
Ответ: 10000.
Выражение в первых скобках раскроем по формуле суммы кубов двух выражений, а деление представим в виде дроби:
Сократим полученную дробь:
Ответ: 130.
Формулы
Сумма и разность кубов двух выражений:
Квадрат суммы двух выражений:
Похожие вопросы
Предмет: Литература,
автор: mewori7
Предмет: Химия,
автор: timasshmatok
Предмет: Музыка,
автор: smesnaasofia51
Предмет: Русский язык,
автор: vsaburova21
Предмет: Биология,
автор: Janaya1905