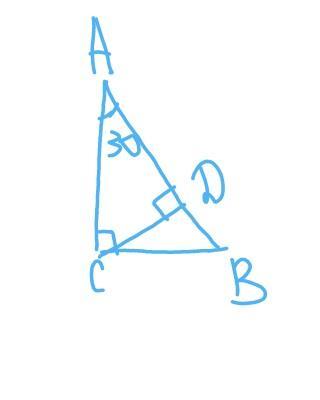прямоугольном треугольнике авс гипотенуза ав равна 12 см,а угол а----30° сд высота опущено из вершины прямого угла с на гипотинкзу ав.нвйдите длинк отрезка ад
Пожалуйста ответьте без рофла очень нужно!!!! прям сейчас если можно
Ответы
Ответ:AD=3 см
Объяснение:Если угол А=60°,то угол В=30°(потому,что прямоугольный треугольник).А напротив угла 30° лежит гипотенуза,которая вдвое больше катета.Тоесть АВ=12,тогда АС=12 АВ=6см треугольник АСD;угол D=90°,угол А=60°,тогда угол АСD=30°.а за теоремой про угол с 30°ми(см.више)АD=12 АС=з см АD=з см
Объяснение:
∆АВС - прямоугольный: ∠С=90° ;
СD - высота ; АВ=12 см ; ∠А=30°
найти : АD
∆АВС :
катет лежащий против угла 30° равен половине гипотенузы:
ВС=АВ:2=12:2=6 см
по теореме Пифагора:
АС=√(АВ²-ВС²)=√(12²-6²)=√108=6√3 см
∆АDC - прямоугольный:
cosA=AD/AC
AD=AC•cos30=6√3•(√3/2)=9 см
ответ: АD=9 cм
проверим другим способом:
∆АВС - прямоугольный:
Катет лежащий против угла 30° равен половине гипотенузы:
ВС=АС:2=12:2=6 см
Сумма острых углов в прямоугольном тр-ке равна 90°
∠В=90-∠А=90-30=60°
∆CDB - прямоугольный:
∠DCB=90-∠B=90-60=30°
катет лежащий против угла 30° равен половине гипотенузы:
ВD=BC:2=6:2=3 см
АD=AB-BD=12-3=9 см
ответ: АD=9 см