(х-2) ² (х² - 4х + 3) < 0
Ответы
(х + 2)² (х² - 4х + 3) < 0
Використаємо метод інтервалів.
Для цього визначимо нулі рівняння (х+2)² (х² - 4х + 3) = 0
Добуток рівний нулю, коли хоча б один з множників дорівнював нулю. Звідси маємо:
(x + 2)² = 0 або х² - 4х + 3 = 0
Розв'язуємо ці рівняння, знаходимо, що
x = 2 або x = 3 або x = 1 (з теореми Вієта)
Зазначу, що корінь 2 є коренем парної кратності, оскільки він має парну степінь, а, отже, при переході через цей корінь, знак виразу не змінюється.
Перепишемо нерівність як
(х - 2)² (х - 1) (x - 3) < 0
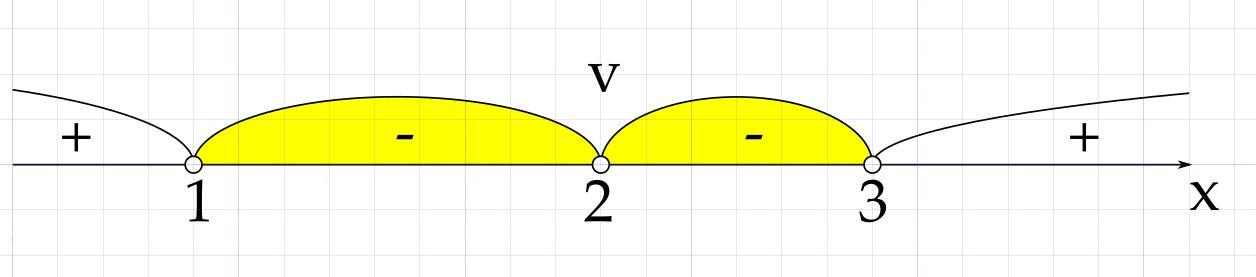
Позначимо ці корені на прямій, роблячи точки виколотими, оскільки нерівність строга. V над коренем означає те, що він парної кратності
Визначимо знак на крайньому правому інтервалі. Для цього можемо піти двома методами:
1) Підстановка значення, більшого за крайній правий нуль. Наприклад, 4.
Маємо 2² · 3 · 1 > 0, тобто плюс.
2) Дивимося знак коефіцієнту біля іксів в множниках непарної парності:
(1·x - 1) ⇒ 1 > 0, (1·x - 3) ⇒ 1 > 0 ⇒ 1 · 1 = 1 > 0 ⇒ Знак - плюс.
Отже, на правому крайньому інтервалі знак плюс. Тоді змінюємо знаки при переході через нулі, які не є коренями парної кратності.
Інтервали, які відповідають умові "більше або рівно нулю": (1;2) та (2;3).
Перепишемо ці два інтеграли як суцільний, з викинутою точкою:
(1;2) ∪ (2;3) ≡ (1;3) / {2}
Відповідь: x ∈ (1;3) / {2}