Question

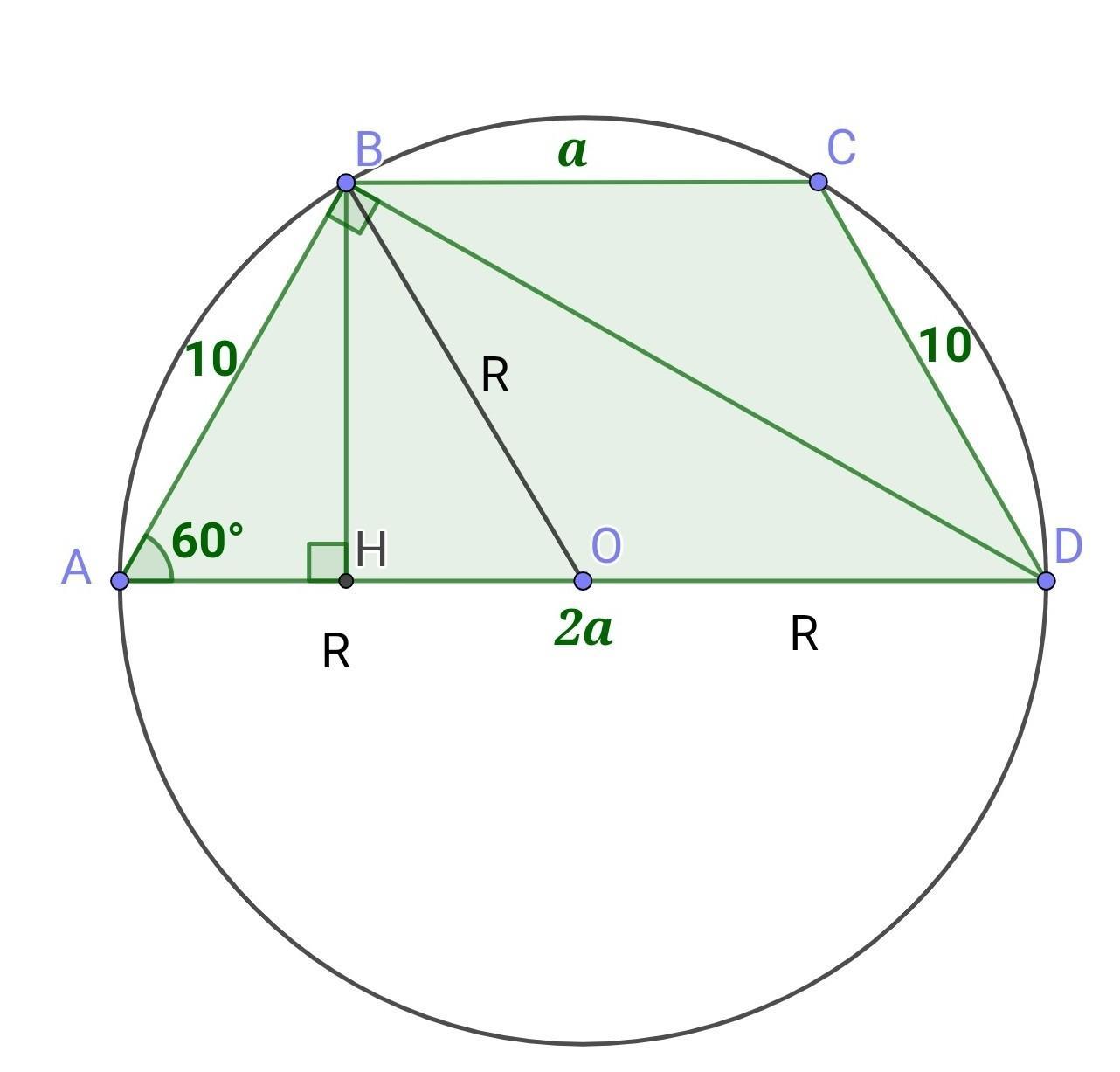
2) Один із кутів вписаної трапеції дорівнює 60°. Знайдіть радіус кола, якщо одна з основ трапеції вдвічі більша за іншу, а бічна сторона дорівнює 10 см.срочно надо желательно с рисунком. даю 100 балов

Answer 1

Ответ:

Радіус кола дорівнює 10 см.

Объяснение:

Один із кутів вписаної трапеції дорівнює 60°. Знайдіть радіус кола, якщо одна з основ трапеції вдвічі більша за іншу, а бічна сторона дорівнює 10 см.

Нехай ABCD дана трапеція, BC||AD, так як трапеція вписана в коло, то вона рівнобічна:

AB=CD=10см.

∠A =∠D = 60° - як кути при основі рівнобічної трапеції.

AD = 2 • BC

Знайдемо радіус описаного кола.

1.

Проведемо висоту ВН. ВН⟂AD.

Розглянемо прямокутний трикутник ABH(∠H=90°)

За властивістю гострих кутів прямокутного трикутника:

∠АВН=90°-∠А=90°-60°=30°

АН = ½ • АВ = ½ • 10 = 5(см) - як катет, що лежить проти кута 30°.

2.

• Висота трапеції, проведена з вершини тупого кута, ділить основу трапеції на два відрізки, менший з яких дорівнює половині різниці основ.

Отже:

$AH = \dfrac{AD - BC}{2} = \dfrac{2BC - BC}{2} = \dfrac{BC}{2}$

Так як АН=5 см, то ВС = 2•АН = 2 • 5 = 10(см).

Тоді AD = 2 • BC = 2 • 10 = 20 (см)

3.

За властивістю трапеції:

∠A + ∠B = 180° , ⇒ ∠B = 180° - 60° = 120°.

∠C = ∠B = 120°- як кути при основі рівнобічної трапеції.

4.

Розглянемо трикутник BCD.

Так як BC = CD = 10 (см), то він рівнобедрений з основою BD.

∠CBD=∠CDB - як кути при основі рівнобедреного трикутника.

За теоремою про суму кутів трикутника маємо:

∠CBD = ∠CDB = ½ • (180°-∠C) = ½ • (180°-20°) = 30°.

5.

∠ABD = ∠B - ∠CBD = 120° - 30° = 90°.

Отже, △ABD - прямокутний, вписаний в коло, як і трапеція ABCD.

AD - його гіпотенуза.

• У прямокутному трикутнику радіус описаного кола дорівнює половині гіпотенузи.

R = ½ • AD = ½ • 20 = 10 (см)

Відповідь: 10 см

#SPJ1