Предмет: Информатика,
автор: danlandan56
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 10 000,
F(n) = n/4 + F(n/4 + 2), если n < 10 000 и n делится на 4,
F(n) = 1 + F(n + 2) , если n < 10 000 и n не делится на 4.
Чему равно значение выражения F(174) – F(3)?
С решением пожалуйста!!!
Ответы
Автор ответа:
0
Ответ:
67
Объяснение:
Для начала найдем, чему будет равно :
Тогда
Автор ответа:
0
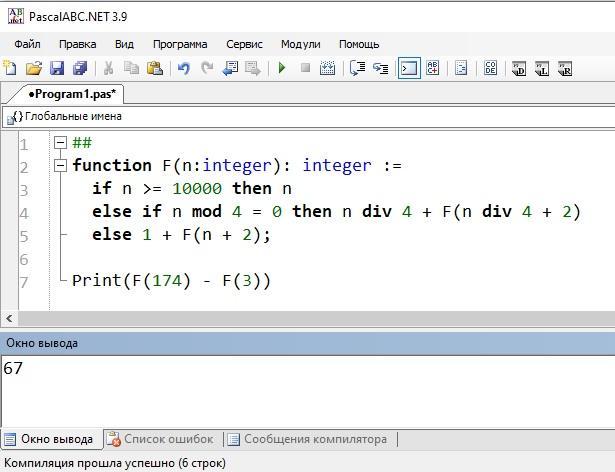
##
function F(n:integer): integer :=
if n >= 10000 then n
else if n mod 4 = 0 then n div 4 + F(n div 4 + 2)
else 1 + F(n + 2);
Print(F(174) - F(3))
Приложения:
Похожие вопросы
Предмет: Математика,
автор: veronikaisaenko935
Предмет: Қазақ тiлi,
автор: anjelina344
Предмет: Қазақ тiлi,
автор: belkodasha1
Предмет: Математика,
автор: goncarenkoalexandr00
Предмет: Алгебра,
автор: qwrsii