Предмет: Алгебра,
автор: FaerVator
помогите с объяснением!
Приложения:
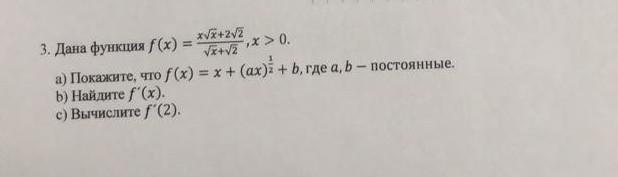
Ответы
Автор ответа:
2
Ответ:
a) Функция имеет вид , отличный от заявленного
b)
c)
Решение:
a) Преобразуем:
Заметим, что функция не имеет заявленный вид , так как для этого должно выполняться равенство
, то есть
, чего быть не может, так как показательная функций не принимает отрицательных значений.
b) Найдем производную функции:
c) Найдем требуемое значение производной:
Элементы теории:
Формула суммы кубов:
Производная суммы и разности:
Производная сложной функции:
Производная степенной функции:
FaerVator:
спасибо)
Похожие вопросы
Предмет: Українська література,
автор: klucko33864
Предмет: Биология,
автор: 15156585
Предмет: История,
автор: kianicapolina001
Предмет: Литература,
автор: alinochkkka67