Question

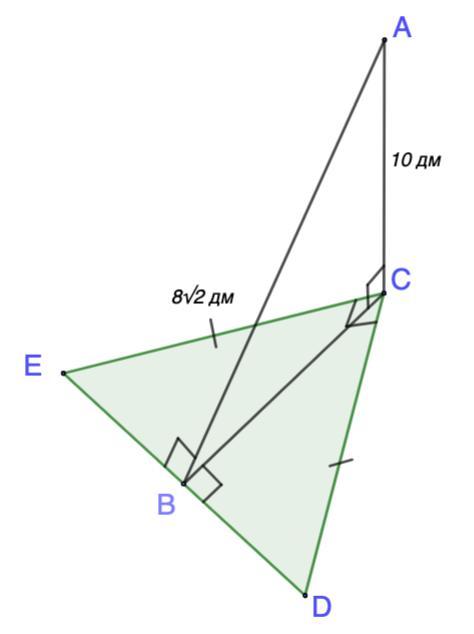
Дан равнобедренный треугольник CDE со стороной CD = 8√2 дм и с прямым углом С. Через вершину С проведена прямая СА перпендикулярная плоскости треугольника и равная СА =10 дм. Найдите расстояние от точки А до прямой DE​

Answer 1

Ответ:

Расстояние от точки А до прямой DE​ равно 2√41 дм.

Объяснение:

Дан равнобедренный треугольник CDE со стороной CD = 8√2 дм и с прямым углом С. Через вершину С проведена прямая СА перпендикулярная плоскости треугольника и равная СА =10 дм. Найдите расстояние от точки А до прямой DE​.

Дано: ΔCDE - прямоугольный, равнобедренный.

∠С = 90°; CD = CE = 8√2 дм;  

АС ⊥ (ЕСD);   AC = 10 дм.

Найти: расстояние от точки А до прямой DE​

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

Проведем АВ ⊥ ЕD. AB ∩ ED = B. Соединим В и С.

АВ - искомое расстояние.

• Прямая, проведенная на плоскости через основание наклонной перпендикулярно ей самой, перпендикулярна и проекции данной наклонной на данную плоскость.

⇒   ВС ⊥ ED

Рассмотрим ΔЕСD - равнобедренный, прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒   ∠Е + ∠D = 90°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠E = ∠D = 45°

Рассмотрим ΔЕСВ - прямоугольный.

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sinE=\frac{CB}{EC} \\\\\frac{\sqrt{2} }{2}=\frac{CB}{8\sqrt{2} }\\ \\ CB=8$(дм)

Рассмотрим ΔВАС - прямоугольный.

• Теорема Пифагора:
• Квадрат гипотенузы равен сумме квадратов катетов.

⇒   АВ² = СВ² + АС² = 64 + 100 = 164   ⇒   АВ = 2√41 дм

Расстояние от точки А до прямой DE​ равно 2√41 дм.

#SPJ1