Предмет: Алгебра,
автор: Tormael123
Решите уравнение:√x+2 + √3-x=3
Приложения:

Ответы
Автор ответа:
0
Ответ:
Иррациональное уравнение .
ООФ:
Возведём обе части равенства в квадрат .
Оба корня входят в ООФ .
Проверка.
Ответ: .
Приложения:
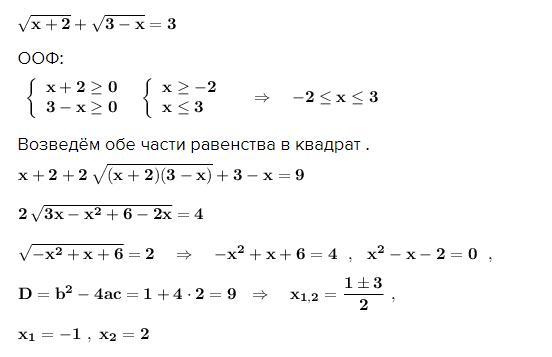
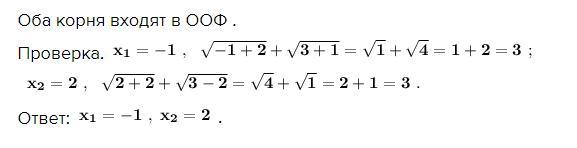
forqforq:
Банальная опечатка испортила вам все решение. Во второй строке вы забыли умножить sqrt((x+2)(x-3)) на 2.
Могли бы не нарушение отмечать , а подсказать , что в ответе на задание опечатка .
Это не я отметил
Да и в любом случае автор уже наврятли бы смог изменить ответ, ибо времени слишком много прошло. Теперь можно понадеяться только на доброго модератора, который отправит ответ на исправление вместо удаления.
Автор ответа:
0
Ответ:
Объяснение:
Во второй строке у вас переход к следующему уравнению не равносилен. По-хорошему нужно было еще ввести ограничение 3 - sqrt(3-x) >= 0 ==> x = [-6; 3] и уже потом возводить в квадрат обе части. Но вам повезло, что решения вошли в это ограничение.
Похожие вопросы
Предмет: Химия,
автор: dajtevoron047
Предмет: Астрономия,
автор: anastasiaefimcuk572
Предмет: Математика,
автор: horbatkina
Предмет: Русский язык,
автор: mirgularman
Предмет: Физкультура и спорт,
автор: arinamuzipova308