2. Стороны прямоугольного треугольника равны 17 см и 16 см. Найдите третью сторону треугольника. Рассмотрите все возможные случаи.
с рисунком!!
Ответы
Відповідь:
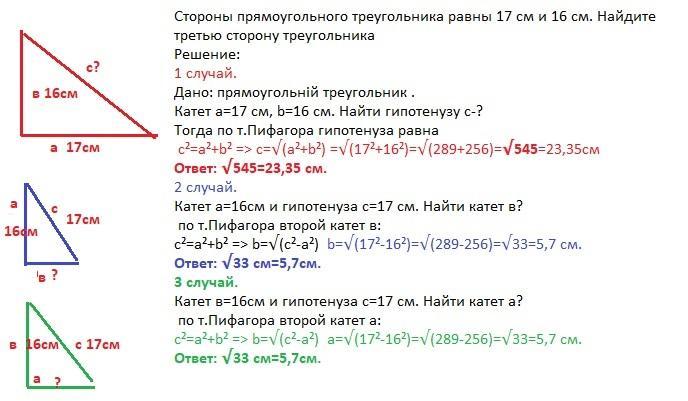
Стороны прямоугольного треугольника равны 17 см и 16 см. Найдите третью сторону треугольника
Решение:
1 вариант.
Дано: прямоугольній треугольник .
Катет а=17 см, b=16 cм. Найти гипотенузу с-?
Тогда по т.Пифагора гипотенуза равна
c²=a²+b² => c=√(a²+b²) =√(17²+16²)=√(289+256)=√545=23,35см
Ответ: √545=23,35 см.
2 вариант
Катет а=16см и гипотенуза с=17 см. Найти катет в?
по т.Пифагора второй катет в:
c²=a²+b² => b=√(c²-a²) b=√(17²-16²)=√(289-256)=√33=5,7 см.
Ответ: √33 см=5,7см.
3 случай.
Катет в=16см и гипотенуза с=17 см. Найти катет а?
по т.Пифагора второй катет а:
c²=a²+b² => b=√(c²-a²) а=√(17²-16²)=√(289-256)=√33=5,7 см.
Ответ: √33 см=5,7см.
Пояснення:
Формула Теоремы Пифагора выглядит так:
a² + b² = c²,
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
a = √c² − b²
b = √c² − a²
c = √a² + b²