Предмет: Геометрия,
автор: Veronikasmagina
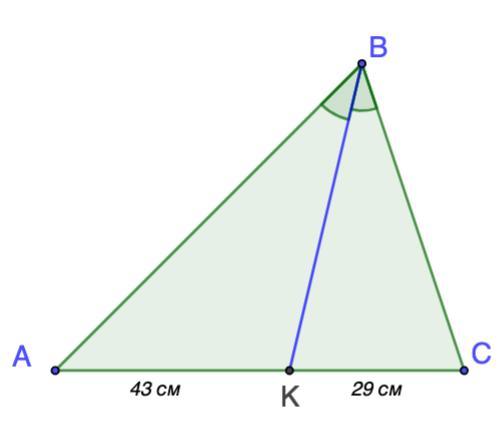
Отрезок ВК-биссектриса угла В треугольника АВС, и делит сторону АС на отрезки 43 см и 29 см. Найти две другие стороны треугольника, если их разность равна 28 см.
Ответы
Автор ответа:
1
Ответ:
Две другие стороны треугольника равны 86 см и 58 см.
Объяснение:
Отрезок ВК-биссектриса угла В треугольника АВС, и делит сторону АС на отрезки 43 см и 29 см. Найти две другие стороны треугольника, если их разность равна 28 см.
Дано: ΔАВС.
ВК - биссектриса;
АК = 43 см; КС = 29 см;
АВ - ВС = 28 см
Найти: АВ и ВС
Решение:
- Биссектриса угла треугольника делит противоположную сторону на части пропорциональные прилежащим сторонам.
Пусть АВ = 43х см, тогда ВС = 29х см.
АВ - ВС = 28 см ⇒ 43х - 29х = 28
14х = 28 |:14
x = 2
⇒ АВ = 86 см; ВС = 58 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Литература,
автор: trwxp56
Предмет: Литература,
автор: zerteer76
Предмет: Математика,
автор: vikusakotusa
Предмет: География,
автор: solihamuxsimova25
Предмет: Геометрия,
автор: nvenera386