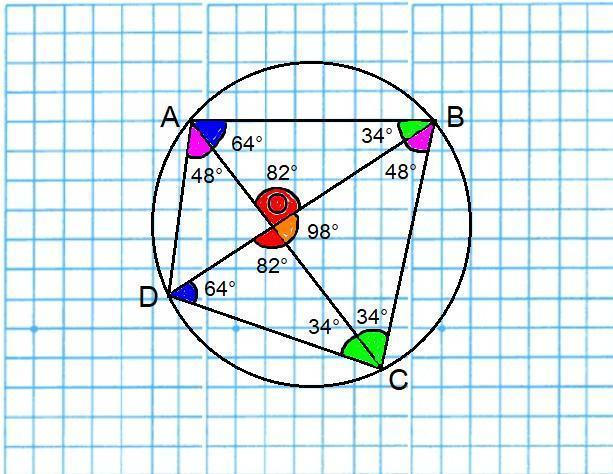
Знайдіть кути чотирикутника ABCD, вписаного в коло, якщо ZCBD=48°,ZACD=34°, BDC=64°.
Ответы
Ответ: ∠A = 112° ; ∠B = 82° ; ∠C = 68° ; ∠D = 98°.
Объяснение: Обозначим середину окружности буквой O.
∠CBD и ∠CAD - вписанные (углы, у которых вершина на окружности, а стороны пересекают окружность).
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
⇒ ∠CBD = ∠CAD = 48°.
COD - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠DOC = 180° - (64° + 34°) = 180° - 98° = 82°.
Сумма смежных углов равна 180°.
⇒ ∠BOC = 180° - 82° = 98°.
COB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠OCB = 180° - (98° + 48°) = 180° - 146° = 34°.
⇒ ∠C = 34° * 2 = 68°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠A = 180° - 68° = 112°.
Если ∠CAD = 48° и ∠A = 112° ⇒ ∠CAB = 112° - 48° = 64°.
Вертикальные углы равны.
⇒ ∠DOC = ∠AOB = 82°.
AOB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠ABO = 180° - (64° + 82°) = 180° - 146° = 34°.
⇒ ∠B = 34° + 48° = 82°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠D = 180° - 82° = 98°.