Діагоналі трапеції ділять її середню лінію на відрізки, довжини яких відносяться як 3:2:3.
Знайти відношення довжин основ трапеції.
Ответы
Ответ:
Основи трапеції відносяться як 3:5
Объяснение:
Діагоналі трапеції ділять її середню лінію на відрізки, довжини яких відносяться як 3:2:3.Знайти відношення довжин основ трапеції.
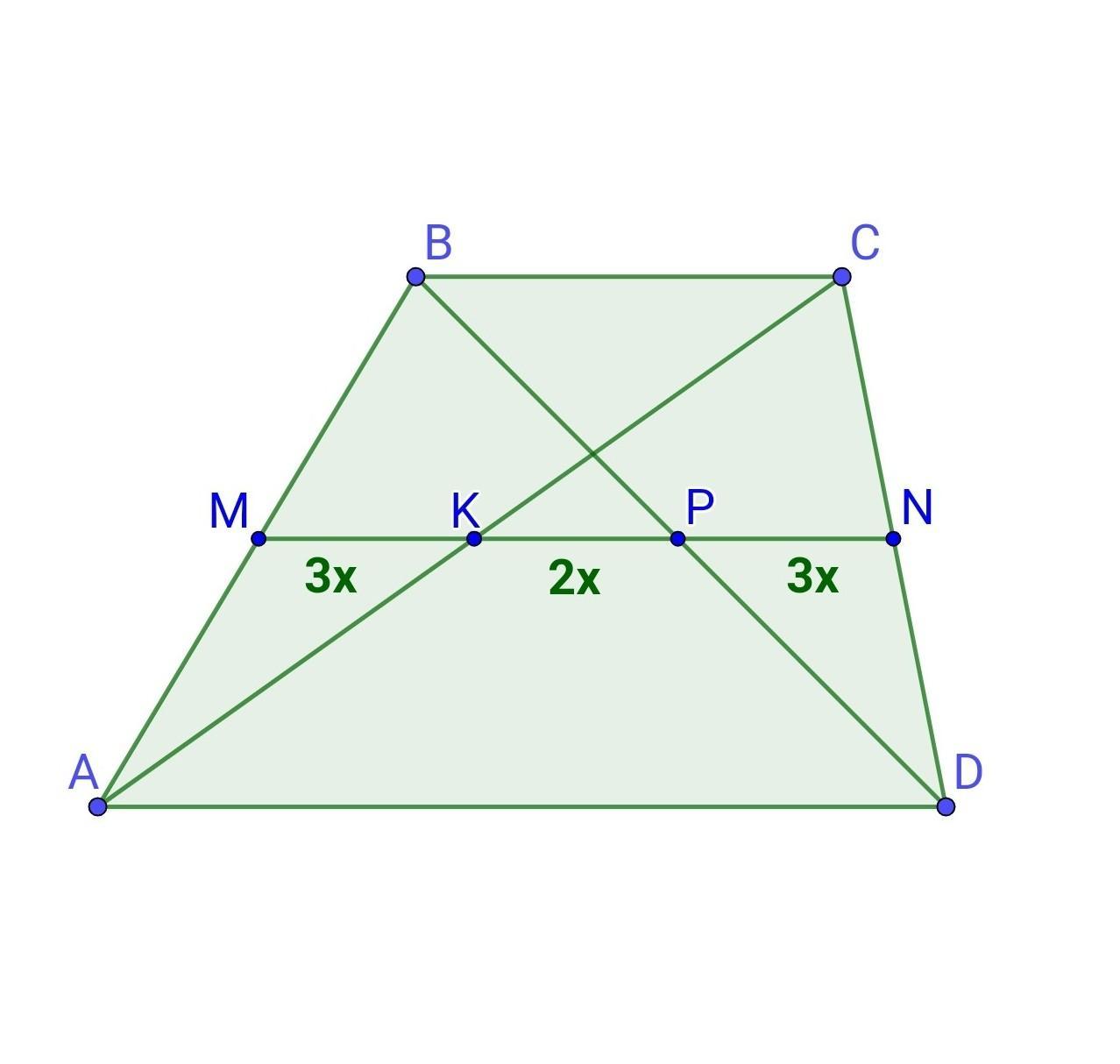
ABCD - дана трапеція, BC||AD, MN - середня лінія, AC і BD - діагоналі, К і Р - точки перетину діагоналей з середньої лінією. MK:KP:PN=3:2:3.
1) Позначимо MK=3x, KP=2x, PN=3x, де х - коефіцієнт пропорційності.
2) У △АВС М - середина сторони АВ, MK||BC (як частина середньої лінії), тоді за теоремою Фалеса точка К - середина сторони АC. Отже, MK - середня лінія трикутника АВС, за властивістю середньої лінії трикутника:
MK=½•BC, ⇒
ВС=2•МК=2•3х=6х
3) У△ACD K - середина сторони AC, N - середина сторони CD. Отже, KN - середня лінія △ACD.
За властивістю середньої лінії трикутника:
KN=½•AD, ⇒
AD=2•KN=2•(KP+PN)=2•(2x+3x)=2•5x=10x.
4) Знайдемо відношення довжин основ трапеції:
Отже, ВС:AD=3:5
#SPJ1