Question

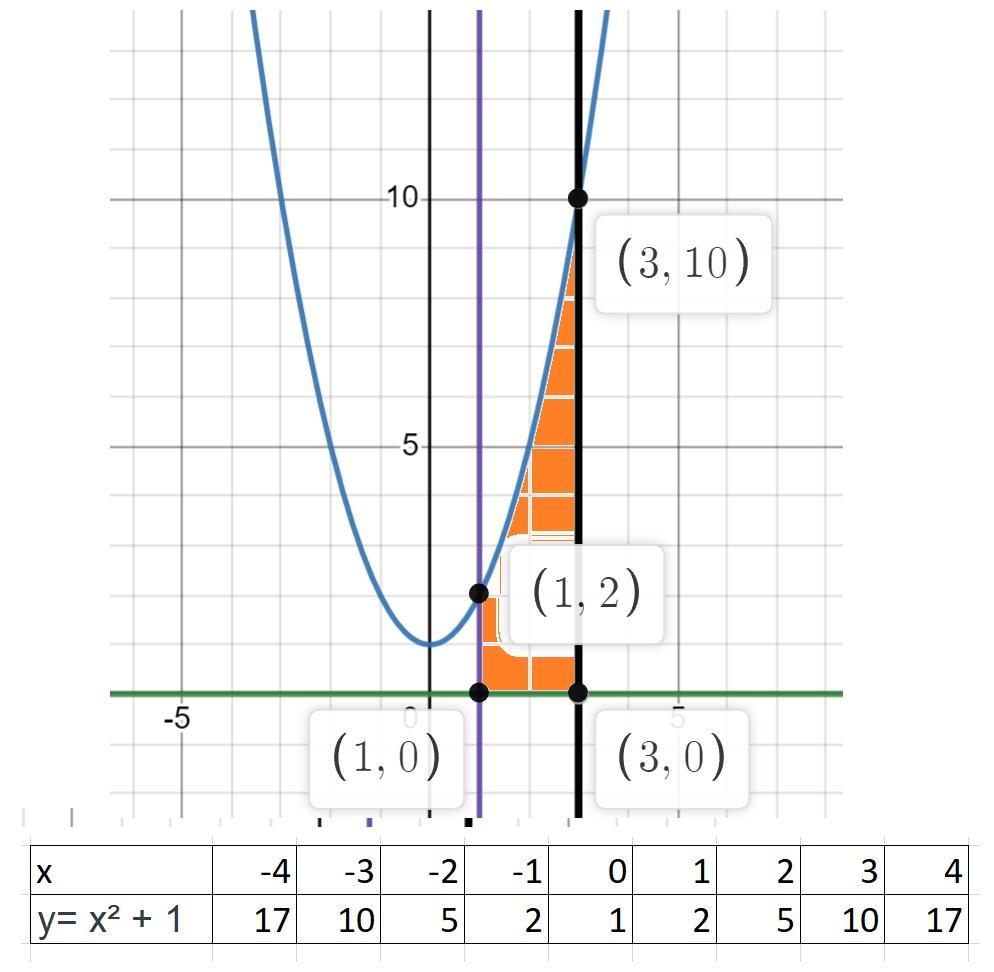
Обчислити площу криволінійної трапеції, обмеженої лініями у= x² + 1; y = 0; x = 1;
х = 3.​

Answer 1

Ответ:             32/3 = 10 2/3 кв. ед.

Пошаговое объяснение:

Строим графики функций у= x² + 1; y = 0;  x = 1;  х = 3.​ (См. скриншот)

Площадь S=∫(a;b)f1(x)dx - f2(x)dx;

Пределы интегрирования a= 1;  b=3.

f1(x) = x^2+1;

f2(x) = 0.  Тогда

∫(1;3) ( x^2+1)dx - 0dx =>

 ∫(1;3) ( x^2+1)dx =   ∫(1;3) x^2dx+∫(1;3) dx = 1/3(x^3)|(1;3) + (x)|(1;3) =

= 1/3(3^3-1^3) + (3-1) = 1/3(27-1) + 2 = 26/3 + 2 = 32/3 = 10 2/3 кв. ед.