Question

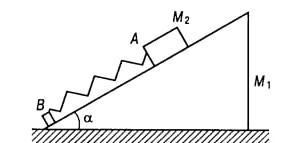
Клин М1 массой 7 кг размещен на гладкой горизонтальной плоскости, угол 30 градусов. Пружина АВ закрепленная в начале клина сжали и отпустили после чего она подняла тело М2 весом 3 кг вверх по наклонной грани клина на расстояние 40 см. Определить расстояние на которое при этом переместился клин.
Должно получиться 19.4 см влево

Answer 1

Ответ:

Для розв'язання цієї задачі використаємо закон збереження енергії. Почнемо з обчислення потенційної енергії пружини після її розтягнення.

Потенційна енергія пружини:

U = 1/2 k x^2

де k - коефіцієнт жорсткості пружини, а x - її розтягнення.

Закон збереження енергії:

U_початкова + K_початкова = U_кінцева + K_кінцева

де U - потенційна енергія, а K - кінетична енергія.

Почнемо з обчислення потенційної енергії пружини після її розтягнення:

U_початкова = 1/2 k x^2

Кінетична енергія тіла М2:

K_кінцева = 1/2 m v^2

де m - маса тіла М2, а v - його швидкість.

Ми також можемо використати взаємозв'язок між переміщенням тіла М2 і переміщенням клина:

x = s sin(α)

де s - переміщення тіла М2, а α - кут нахилу клина.

Тепер ми можемо записати рівняння збереження енергії:

U_початкова + 0 = 0 + K_кінцева

1/2 k x^2 = 1/2 m v^2

Також, ми можемо використати рівняння руху тіла М2:

v^2 = u^2 + 2 a s

де u - початкова швидкість тіла М2, а a - прискорення тіла М2.

Так як тіло М2 починає свій рух з нульовою швидкістю, то u = 0.

Прискорення тіла М2 можна знайти за допомогою другого закону Ньютона:

F = m a

де F - сила, яку додає пружина, а a - прискорення тіла М2.

Сила, яку додає пружина, можна знайти за допомогою закону Гука:

F = k x

Тепер ми можемо записати рівняння для прискорення тіла М2:

k x = m a

a = k x/m

Також, ми можемо виразити швидкість тіла М2 через прискорення:

v^2 = 2 a s

v^2 = 2 ·k x/m s

Підставимо це в рівняння збереження енергії:

1/2 k x^2 = 1/2 m · 2 ·k x/m s

k x^2 = k x s

x = s

Отже, ми отримали, що переміщення клина дорівнює переміщенню тіла М2. Таким чином, переміщення клина дорівнює 40 см, як і переміщення тіла М2.