Предмет: Математика,
автор: anna48088
Дужеее треба
Даю 25 балів
Приложения:
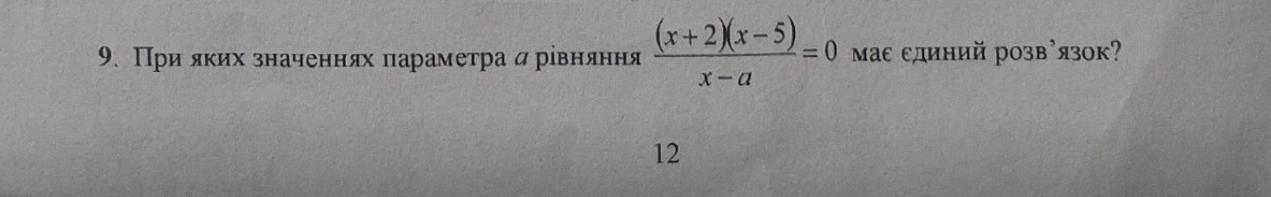
Ответы
Автор ответа:
0
Ответ:
Щоб рівняння ((x + 2)(x - 5))/(x - a) = 0 мало один єдиний розв'язок, дробовий вираз має дорівнювати нулю, проте знаменник не може бути рівний нулю, оскільки ділення на нуль не визначено.
Отже, розв'язком цього рівняння буде значення х, що призводить до чисельника (x + 2)(x - 5) дорівнює нулю.
Розкладаємо чисельник (x + 2)(x - 5):
(x + 2)(x - 5) = 0
Тепер ми можемо визначити значення х, якщо один з множників (x + 2) або (x - 5) дорівнює нулю:
x + 2 = 0 => x = -2
або
x - 5 = 0 => x = 5
Отже, щоб рівняння ((x + 2)(x - 5))/(x - a) = 0 мало єдиний розв'язок, параметр а має приймати значення -2 або 5.
Похожие вопросы
Предмет: История,
автор: tkacenkovaleria390
Предмет: Алгебра,
автор: wetsii
Предмет: Українська мова,
автор: otsskijdima2
Предмет: Биология,
автор: Kisa0921
Предмет: Математика,
автор: 555haiKai