Предмет: Геометрия,
автор: ljubasik26
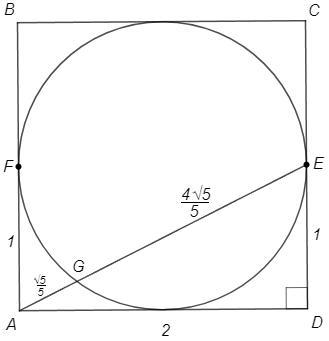
.У квадрат ABCD зі стороною а вписано коло, яке дотикається сторони CD у точці Е. Знайти хорду, що з'єднує точки, в яких коло перетинається з прямою AЕ.
Ответы
Автор ответа:
0
Теорема о касательной и секущей:
Квадрат касательной (AF) равен произведению секущей (AE) на ее внешнюю часть (AG).
Пусть сторона квадрата 2.
AD=2
Окружность касается сторон в их серединах.
AF=DE=1
Теорема Пифагора:
AE =√(AD^2+DE^2) =√5
Теорема о касательной и секущей:
AF =AE*AG => 1 =√5 AG => AG=1/√5 => GE =4/√5
По условию сторона квадрата =a.
GE =4/√5 *a/2 =2a/√5
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: zajceva323t
Предмет: Қазақ тiлi,
автор: leylasm19
Предмет: Другие предметы,
автор: arturmisalkin
Предмет: Русский язык,
автор: egorychsarsembayev
Предмет: Геометрия,
автор: kuvichavaleriya