Предмет: Алгебра,
автор: angelenina090405
Алгебра 40 баллов,пожалуйста
Приложения:

Ответы
Автор ответа:
0
Объяснение:
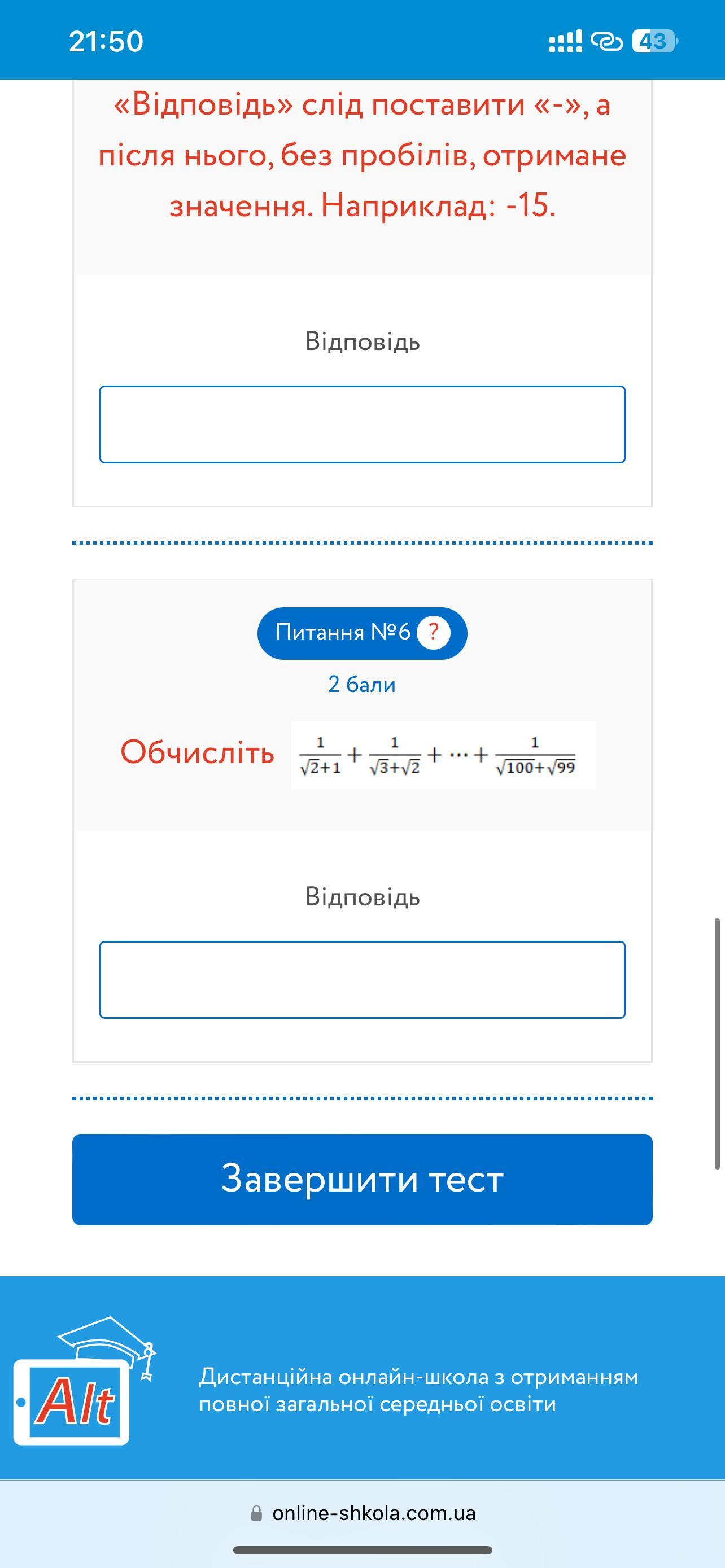
Бачимо, що все взаємо-знищується і залишається лише -1 та . Отже, весь цей вираз дорівнює - 9
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mansursarsen09
Предмет: Алгебра,
автор: gamag1728
Предмет: Физика,
автор: sgsusl
Предмет: Қазақ тiлi,
автор: medinazasulan01