Question

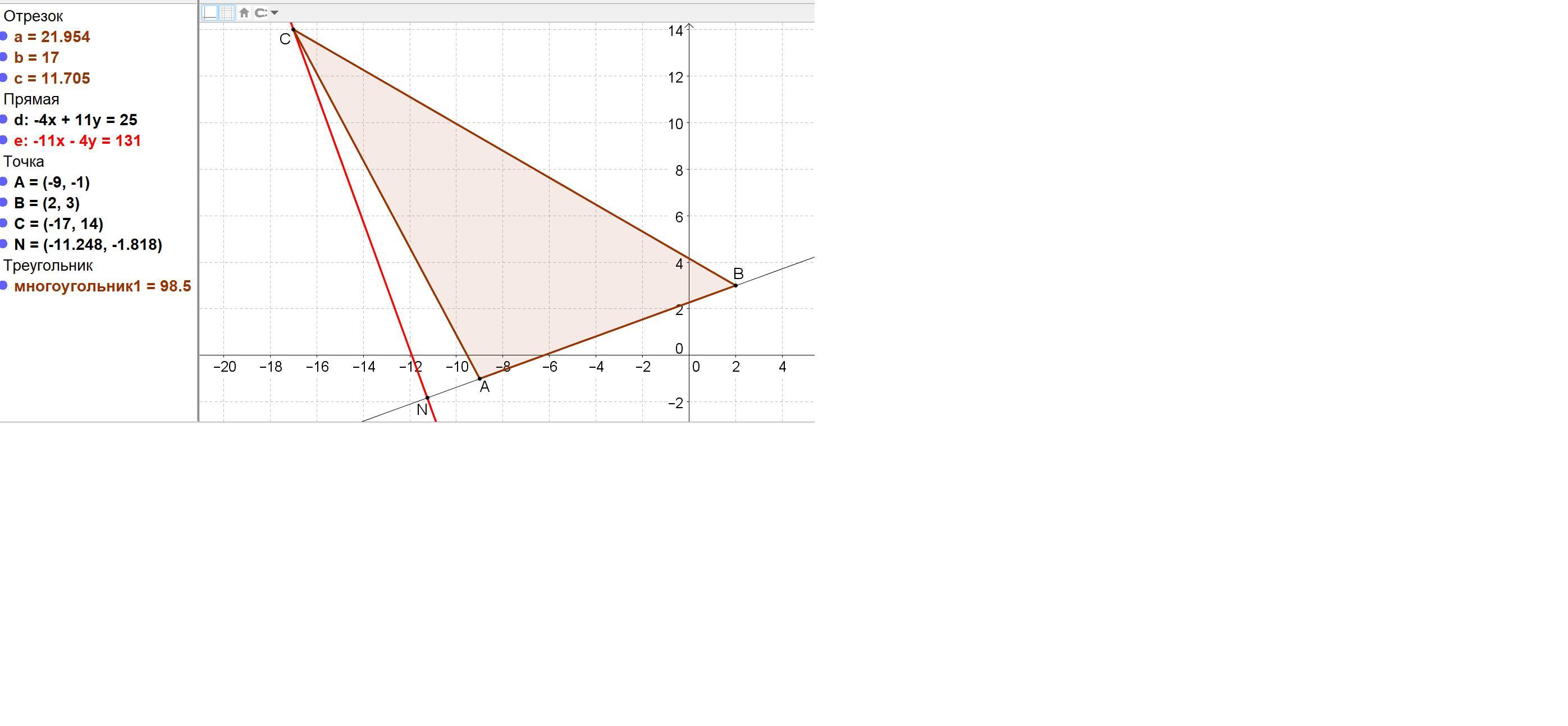
Даны вершины треугольника АBC: A(-9;-1) B(2;3) C(-17;14). Найти уравнение высоты CN и точку N её пересечения со стороной AB

Answer 1

Даны вершины треугольника АBC: A(-9;-1), B(2;3), C(-17;14). Найти уравнение высоты CN и точку N её пересечения со стороной AB.

Вектор АВ = B(2;3) - A(-9;-1) = (11; 4).

Уравнение АВ:

(х + 9)/11 = (у + 1)/4 каноническое.

4х + 36 = 11у + 11,

4х – 11у + 25 = 0 общее в виде Ах + Ву + С = 0.

Высота CN – это перпендикуляр к стороне АВ.

У перпендикулярной прямой коэффициенты А и В меняются на В и (-А) или

(-В) и А.

Уравнение CN: 11х + 4у + С = 0. Для определения параметра С подставим координаты точки C(-17;14).

11*(-17) + 4*14 + С = 0, отсюда С = 187 – 56 = 131.

Уравнение CN: 11х + 4у + 131 = 0.

Координаты точки N находим из системы:

{4х – 11у + 25 = 0,        (x4) = 16х – 44у + 100 = 0,

{11х + 4у + 131 = 0,   (x11) = 121x + 44y + 1441 = 0.  

                                              137x           + 1541 = 0,

                                                    x = -1541/137 = -11,248175.

y = (4x + 25)/11 = (4*(-1541/137) + 25)/11 = (-2739/1507) = -1,817518.