Предмет: Алгебра,
автор: LerixC
Помогите пожалуйста срочно!!
Приложения:
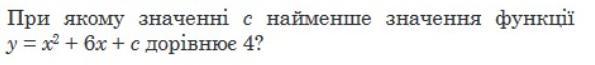
Ответы
Автор ответа:
0
Ответ:
Щоб знайти найменше значення функції \( у = х^2 + 6х + с \), вам потрібно взяти похідну цієї функції за \( х \) і прирівняти її до нуля. Після цього вирішіть рівняння для \( х \), і вставте це значення у вихідну функцію, щоб знайти відповідне значення \( у \).
\[ у' = 2x + 6 \]
Прирівняємо до нуля та розв'яжемо рівняння:
\[ 2x + 6 = 0 \]
Отримаємо \( x = -3 \).
Тепер підставимо \( x = -3 \) у вихідну функцію:
\[ у = (-3)^2 + 6(-3) + с \]
Отримаємо \( у = с - 9 \).
Таким чином, при \( с = 9 \) функція приймає найменше значення, яке дорівнює 0.
Похожие вопросы
Предмет: История,
автор: alniyaz
Предмет: Математика,
автор: l38490164
Предмет: История,
автор: zhakupbekovaaman
Предмет: Математика,
автор: Xalivza
Предмет: Математика,
автор: samarskayall