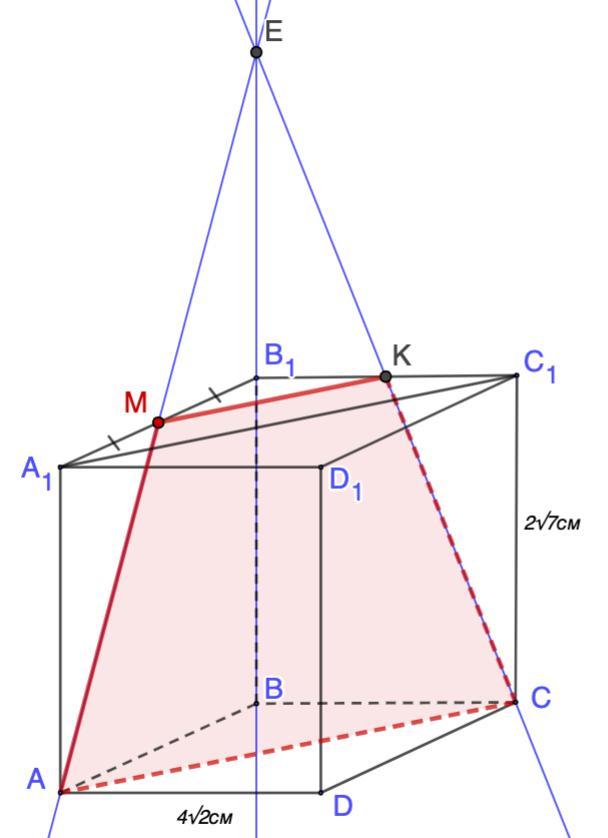
Дан параллелепипед ABCDA1B1C1D1, два противоположных основания которого, ABCD и A1B1C1D1 являются квадратами со стороной 4√2 см, а остальные грани - прямоугольниками. Известно, что СС1 - 2√7 см. На стороне А1В1 отметили точку М так, что А1М = MB1 Найдите периметр сечения параллелепипеда плоскостью АМС.
Ответы
Ответ:
Периметр сечения равен 24 см.
Объяснение:
Дан параллелепипед ABCDA₁B₁C₁D₁, два противоположных основания которого, ABCD и A₁B₁C₁D₁ являются квадратами со стороной 4√2 см, а остальные грани - прямоугольниками. Известно, что СС₁ = 2√7 см. На стороне А₁В₁ отметили точку М так, что А₁М = MB₁. Найдите периметр сечения параллелепипеда плоскостью АМС.
Дано: ABCDA₁B₁C₁D₁ - параллелепипед;
ABCD и A₁B₁C₁D₁ - квадраты; АВ = 4√2 см;
СС₁ - 2√7 см;
М ∈ А₁В₁; А₁М = MB₁.
Найти: Р сечения плоскостью АМС;
Решение:
1. Построим сечение.
А ∈ (АА₁В₁); М ∈ (АА₁В₁) ⇒ А и М - соединяем.
АМ ∩ ВВ₁ = Е;
Е ∈ (ВВ₁С₁); С ∈ (ВВ₁С₁) ⇒ Е и С - соединяем.
ЕС ∩ В₁С₁ = К.
АМКС - сечение.
2. (АЕС) ∩ (А₁В₁С₁) = МК; (АЕС) ∩ (АВС) = АС
- Если две параллельные плоскости пересечены третьей, то линии пересечения будут параллельны.
(А₁В₁С₁) || (ABC) ⇒ MK || AC
- Если две прямые параллельны третьей, то они параллельны между собой.
АС || A₁C₁; MK || AC ⇒ MK || A₁C₁.
3. Рассмотрим ΔА₁В₁С₁.
По теореме Пифагора:
А₁С₁² = А₁В₁² + В₁С₁² = 64 ⇒ А₁С₁ = 8 см
А₁М = МВ₁; МК || A₁C₁
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
⇒ МК - средняя линия.
- Средняя линия равна половине стороны, которую она не пересекает.
⇒ МК = 4 см.
4. Из ΔАА₁М найдем АМ.
А₁М = 2√2 см, АА₁ = 2√7 см
По теореме Пифагора:
АМ² = А₁М² + АА₁² = 8 + 28 = 36 ⇒ АМ = 6 см
5. Найдем периметр АМКС.
- Периметр - сумма длин всех сторон.
Р(АМКС) = 6 + 4 + 6 + 8 = 24 (см)
Периметр сечения равен 24 см.
#SPJ1