Question

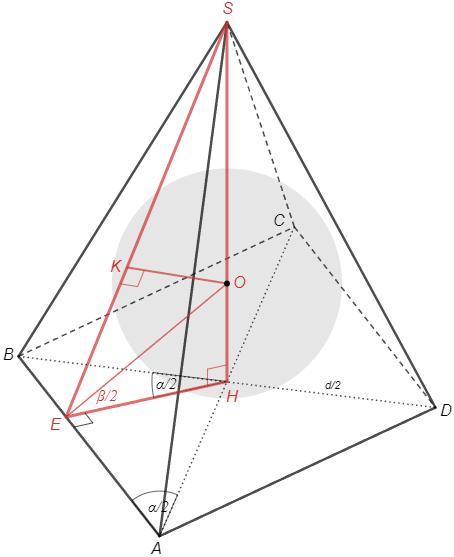
Основою піраміди є ромб з гострим кутом а, а його менша діагональ дорівнює д. Кожний двогранний кут піраміди при ребрі основи дорівнює В. Знайдіть радіус кулі, вписаної в дану піраміду.​

Answer 1

Ответ:

R = $\frac{d }{2} cos\frac{\alpha}{2} tg\frac{\beta}{2}$

Решение:

SH⊥(ABC), HE⊥AB => SE⊥AB (т о трех перпендикулярах)

∠SEH =∠(SE;HE) =b (линейный угол двугранного угла SABC)

Если мы проведем перпендикуляры из H к другим сторонам и построим треугольники, аналогичные SEH, то они будут равны по катету (высота пирамиды) и острому углу (двугранный угол при ребре). Точка H равноудалена от сторон основания и является точкой пересечения диагоналей ромба.

(Убедились, что если грани пирамиды наклонены к основанию под равными углами, то вершина падает в центр вписанной окружности основания.)

EO - биссектриса ∠SEH

OK⊥SE

OK=OH (любая точка на биссектрисе равноудалена от сторон угла)

AB⊥(SEH) => OK⊥AB => OK⊥(SAB)

OK - расстояние от O до плоскости SAB

Аналогично расстояние от O до других граней равно ОН. Точка O равноудалена от всех граней и является центром вписанного шара.

Стороны ромба равны. По т косинусов против меньшего угла лежит меньшая диагональ. ∠BAD=a, BD=d

∠BAH =a/2 =∠BHE

EH =BH cos(BHE) =d/2 cos(a/2)

OH =EH tg(OEH) =d/2 cos(a/2) tg(b/2)