Предмет: Алгебра,
автор: ayxanbayramov195
Помогите пожалуйста не могу решить
Приложения:

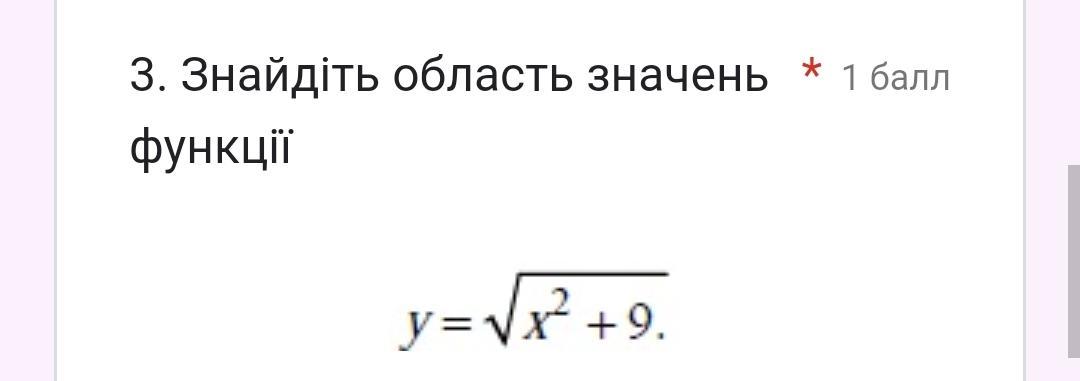

Ответы
Автор ответа:
0
Объяснение:
1)
ОДЗ:
Проверка:
Ответ: x=6.
2)
ОДЗ:
-∞__+__-3__-__3__+__+∞ ⇒
y∈(-∞;-3]U[3;+∞).
Согласно ОДЗ:
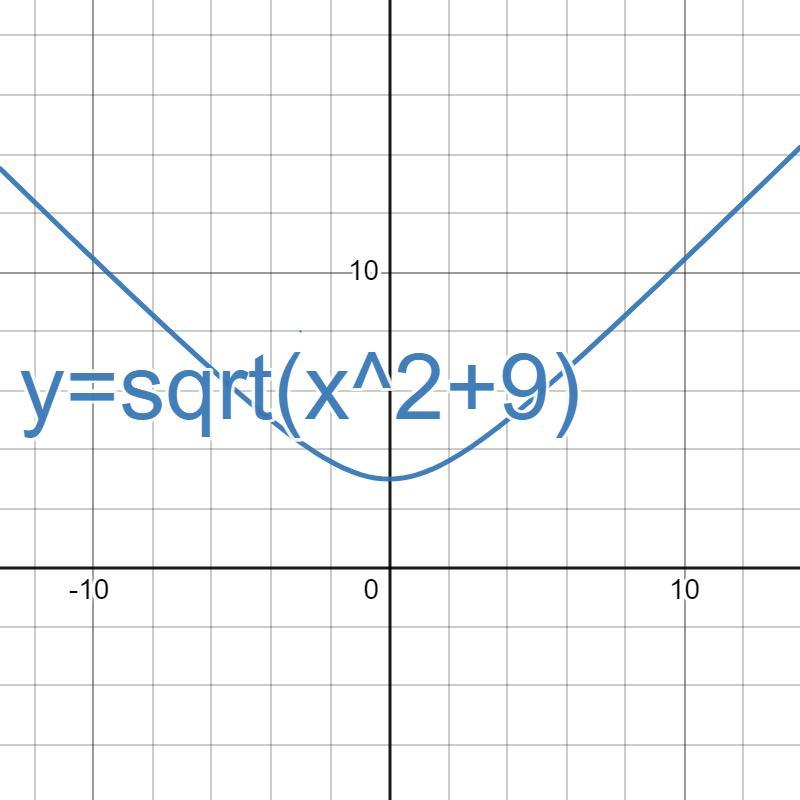
Ответ: y∈[3;+∞).
3)
Приложения:
Похожие вопросы
Предмет: География,
автор: screan91148
Предмет: Английский язык,
автор: kapitohamer
Предмет: Физика,
автор: genshinssakk
Предмет: Қазақ тiлi,
автор: karaevagulnaz77750
Предмет: Физика,
автор: dilnarailesken