Предмет: Алгебра,
автор: vitalyna2009
СРОЧНО!!! ПОМОГИТЕ РЕШИТЬ
Приложения:
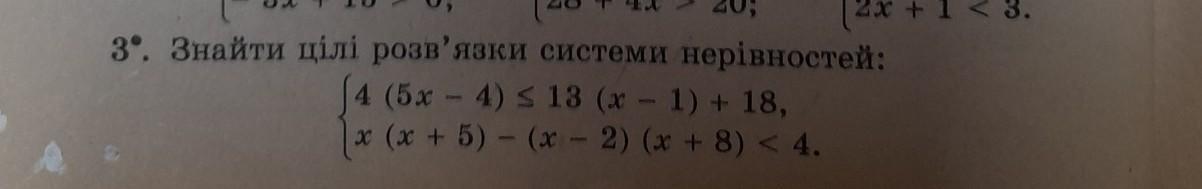
Ответы
Автор ответа:
0
Відповідь:
x є (-∞: 3] V (12; +∞), x є n (якщо ви не знаєте що таке n, і ви його не проходили - вам краще його не писати)
Пояснення:
Розкриваємо дужки:
Зведено подібні доданки:
Відкриємо дужки:
Заходимо подібні доданки:
Тепер невідомі в одну сторону, а відомі в іншу:
Зводимо подподібні доданки:
Знаходимо x (нагадую в нижньому рівнянні ми множимо ообидві частини на -1 і перевертаємо знак на протилежний)
Відповідь: x є (-∞: 3] V (12; +∞) (Дужка при трійці кквадратна тому, що там знак менше РІВНЕ)
Похожие вопросы
Предмет: Химия,
автор: irynakalahan
Предмет: Русский язык,
автор: ademiintykbai04
Предмет: Українська література,
автор: arsen1324
Предмет: Алгебра,
автор: urbanurij01
Предмет: История,
автор: hamidovaelita