1) В равнобедренной трапеции ABCD с основаниями AD = 17 см,
ВС = 5 см и боковой стороной АВ = 10 см через вершину В проведена пря-
мая, делящая диагональ АС пополам и пересекающая основание AD в точке
М. Найдите площадь треугольника BDM.
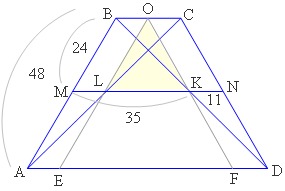
2)Боковая сторона равнобедренной трапеции равна 48 см, а средняя
линия делится диагональю на два отрезка, равных 11 см и 35 см. Найдите
углы трапеции.
Ответы
2)
Проведём ОЕ и ОF параллельно боковым сторонам через точки пересечения средней линии трапеции с её диагоналями.
ОЕ и ОF пересекутся в точке О на основании ВС, так как находятся на расстоянии 11см от боковых сторон,
а верхнее основание ВС=22см. (Это легко вычислить, используя подобие тр. МВК и АВD)
Получившийся треугольник LOK равносторонний (каждая сторона равна 24см) и, следовательно, его углы равны по 60град.
Отсюда ясно, что углы трапеции при большем основании также равны по 60град. (соответственные углы при параллельных прямых).
Углы трапеции при верхнем основании равны по 180-60=120град.