Предмет: Алгебра,
автор: VSEbude
Даю 100 балов
Розв'яжіть системи рівнянь
Приложения:

Ответы
Автор ответа:
3
Ответ:
Решить системы уравнений . Применяем замену переменной .
1)
Обратная замена.
Сложим уравнения системы и вычтем из 1уравнения второе .
2)
Обратная замена .
Вычтем из второго уравнения первое .
Вычтем из второго уравнения первое .
Ответ: .
Приложения:


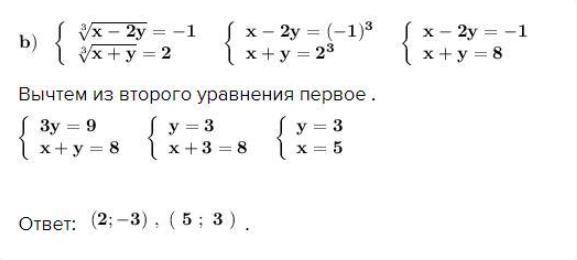
kardibalet:
помогите с заданиями в моем профиле, пожалуйста
Похожие вопросы
Предмет: Українська мова,
автор: HatiKILLER
Предмет: Математика,
автор: y9too
Предмет: География,
автор: olichkasonichka4
Предмет: Химия,
автор: Aidar92637
Предмет: Немецкий язык,
автор: 1234563434343