Предмет: Алгебра,
автор: gamerden132
Доведіть тотожність.
Мені потрібно те як воно вирішується! Тільки відповідь не підійде, мені рішення потрібно щоб ви розписали й сфоткав відправили, або в самій відповіді написали все щоб було зрозуміло де який знак.
Приложения:
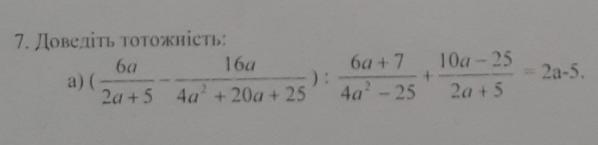
Ответы
Автор ответа:
1
Ответ:
Смотри решение на фото...
Приложения:
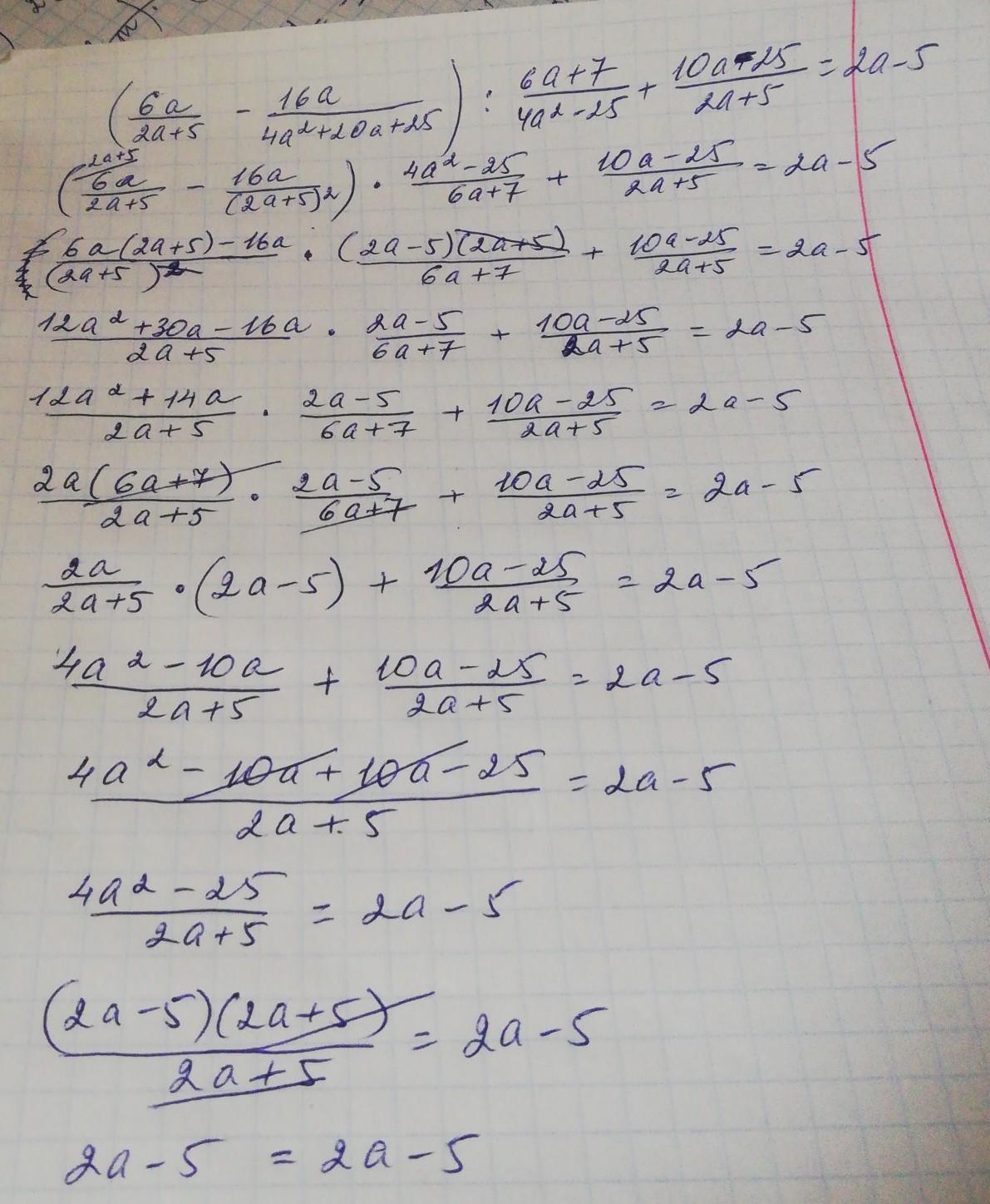
gamerden132:
блягодарю
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: История,
автор: nikse0909
Предмет: Биология,
автор: maleeva31101985
Предмет: Українська література,
автор: kirpicovvolodimir9
Предмет: Физика,
автор: kvkv5363