Предмет: Математика,
автор: peremogavsov
6.16 завдання.........
Приложения:
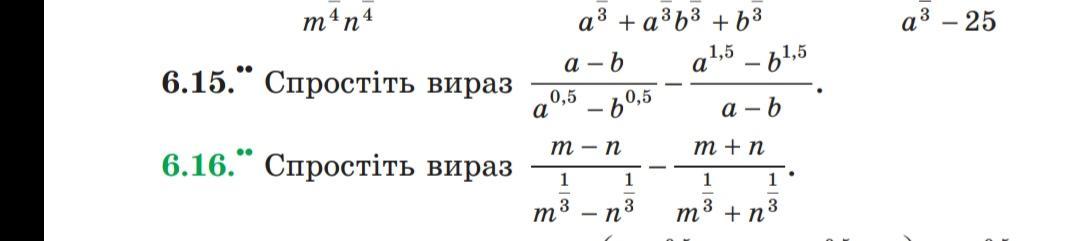
Ответы
Автор ответа:
1
Для спрощення виразу скористаємося формулою різниці квадратів для спрощення дробів.
Спочатку розглянемо перший дріб:
Тепер розглянемо другий дріб:
Тепер віднімемо другий дріб від першого:
Отже, спрощений вираз дорівнює
Похожие вопросы
Предмет: Русский язык,
автор: yusifmammadli57
Предмет: Математика,
автор: natashalicevich
Предмет: Геометрия,
автор: mariannatrikoz
Предмет: География,
автор: nikch2007