Question

ДОПОМОЖІТЬ, БУДЬ ЛАСКА!!!
У трикутнику ABC відомо, що BA=AC=15см, кут ABC=50*. На бісектрисі кута В позначили таку точку К, що кут ВСК=115*. Знайдіть відрізок АК

Answer 1

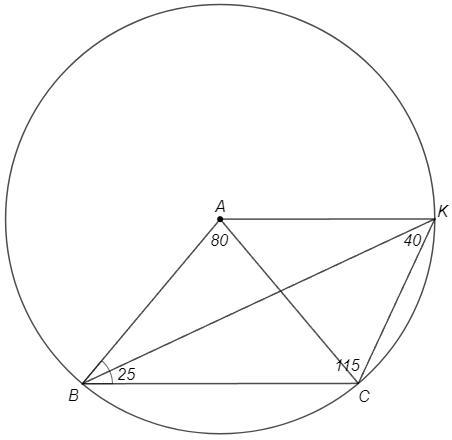
∠KBC =∠ABC/2 =50°/2 =25° (BK - биссектриса)

∠BKC =180°-∠KBC-∠BCK =180°-25°-115° =40°

∠BAC =180°-2∠ABC =180°-50°*2 =80° (△ABC - р/б, ∠ABC=∠ACB)

Отрезок BC виден из точки A под углом 80°, а из точки K под вдвое меньшим углом 40°, следовательно точки K, B, C лежат на окружности с центром A (∠BAC - центральный угол, ∠BKC - вписанный угол).

AK=AB=15 (см)