Предмет: Геометрия,
автор: anisargsyaannn
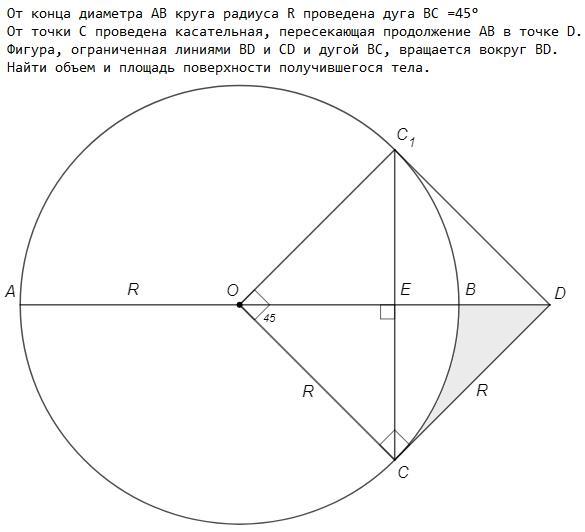
От конца диаметра АВ полукруга радиуса R проведена дуга ВМС, содержащая 45°, а от точки С проведена касательная, пересекающая продолжение диаметра АВ в точке D. Изображение, ограниченное линиями BD и CD и дугой BMC, вращается вокруг BD. Определите объем и площадь поверхности получившегося тела.
Ответы
Автор ответа:
1
Точка С1 симметрична C относительно AD.
OCDC1 -квадрат
DE =CE =R √2/2
BE =OB-OE =R(2-√2)/2
Фигура - разность конуса (высота DE, радиус основания CE) и шарового сегмента (высота BE, радиус R).
Конус Объем
Vк =1/3 DE п CE^2 =пR^3 √2/12
Шаровой сегмент Объем
Vшс =п BE^2 (R -BE/3) =пR^3 (8-5√2)/12
Искомый объем
V = Vк-Vшс =пR^3 (3√2-4)/6
Конус Площадь бок.
Sбк =п CE CD = пR^2 √2/2
Шаровой сегмент Площадь
Sшс =2п R BE =пR^2 (2-√2)
Искомая площадь - сумма боковой поверхности конуса и площади шарового сегмента.
S = Sбк+Sшс =пR^2 (2 -√2/2)
Приложения:
anisargsyaannn:
вы гений! спасибо!
Похожие вопросы
Предмет: Другие предметы,
автор: vadoskorotenko
Предмет: Английский язык,
автор: dimasikpro2011
Предмет: Немецкий язык,
автор: sofiamerkylova58
Предмет: Геометрия,
автор: zhanko120508
Предмет: История,
автор: weipwtele