2. В ∆ABC проведена биссектриса AD, а через точку D прямая, параллельная AC и пересекающая AB в точке Е. Найдите отношение площадей ∆ABC и ∆BDE, если AB = 5, AC = 7.
Прошу, помогите...
Ответы
Объяснение:
лови пупсик,недаюсь помогла
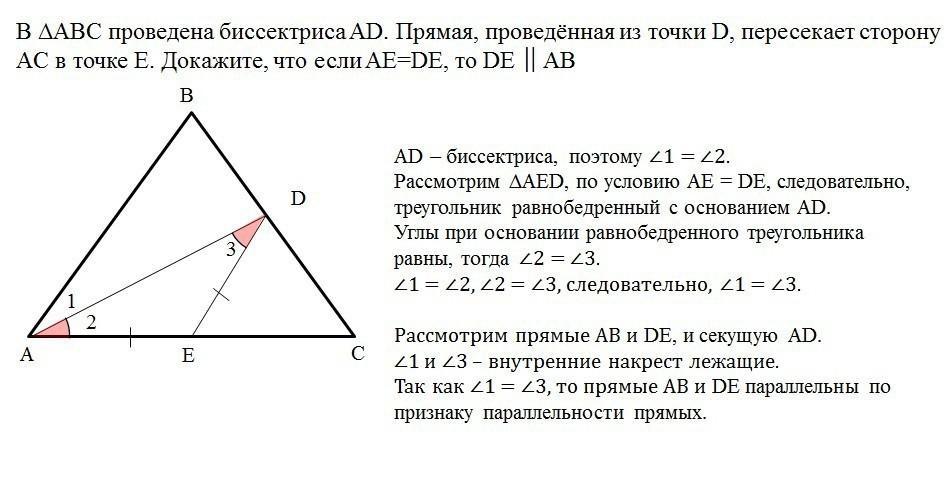
Ответ:
Для решения данной задачи воспользуемся свойствами биссектрисы треугольника.
1. Из свойства биссектрисы известно, что отрезок BD делит сторону AC треугольника AABC пропорционально отношению других двух сторон:
BD/DC = AB/AC.
2. Из условия задачи известно, что BD параллельна AC, поэтому треугольники ABD и ACD подобны, и мы можем записать следующую пропорцию:
AD/DC = AB/AC.
3. Из полученных двух пропорций можно найти отношение AD/BD:
AD/BD = (AD/DC) / (AB/AC) = (AB/AC) / (AB/AC + 1) = 1 / (AB/AC + 1).
4. Из пропорции AC = 7 и AB = 5 можем найти AD:
AD/DC = AB/AC,
AD/DC = 5/7,
AD = DC * 5/7.
5. Найдем отношение площадей треугольников AABC и ABDE. Заметим, что треугольники AAB и ADE имеют общую высоту, поэтому отношение их площадей равно отношению их оснований: AD/AB.
6. Подставим найденное выражение для AD:
AD/AB = (DC * 5/7) / AB = DC * 5 / (7 * AB),
AD/AB = 5/7 * DC / AB.
7. Из условия задачи известно, что AB = 5, поэтому AD/AB = 5/7 * DC / 5 = DC/7.
Таким образом, отношение площадей треугольников AABC и ABDE равно DC/7. Осталось только найти отрезок DC.
Из первой пропорции BD/DC = AB/AC, подставим значения:
BD/DC = 5/7,
BD = 5DC/7.
Из условия задачи известно, что AB = 5, поэтому BC = AB - AC = 5 - 7 = -2. Отрицательное значение говорит о том, что точка C находится левее точки B. В таком случае, отрезок DC равен сумме отрезков BD и BC:
DC = BD + BC = 5DC/7 - 2.
Решим уравнение:
7DC = 5DC - 14,
2DC = -14,
DC = -7.
Таким образом, DC = -7.
Подставим найденное значение DC в формулу для отношения площадей:
отношение площадей AABC и ABDE = DC/7 = (-7)/7 = -1.
Отношение площадей треугольников AABC и ABDE равно -1.