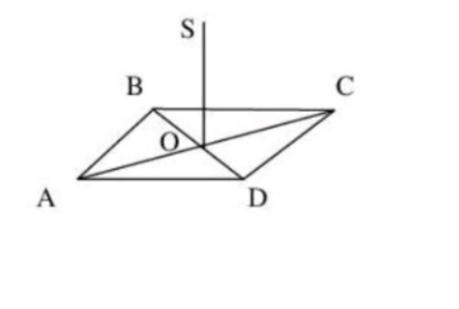
Із точки О перетину діагоналей прямокутника АВСD проведено
перпендикуляр ЅО до площини (АВС). Знайдіть ЅА, якщо SO = 6см, BD = 16см
Ответы
Для розв'язання цієї задачі використаємо властивість прямокутника: діагоналі взаємно діляться навпіл.
Позначимо половину довжини діагоналі BD як \( \frac{BD}{2} \). Оскільки прямокутник, то діагоналі взаємно перпендикулярні, і точка О - їх перетин. Також, оскільки SO - це висота, проведена з точки O до площини ABC, то трикутник SOB є прямокутним.
За теоремою Піфагора для трикутника SOB:
\[ SB^2 + \left(\frac{BD}{2}\right)^2 = SO^2 \]
Підставимо відомі значення:
\[ SB^2 + 8^2 = 6^2 \]
Розв'яжемо для SB:
\[ SB^2 = 36 - 64 = -28 \]
Отже, SB - це комплексне число, що не має реального значення у контексті довжини. Це свідчить про те, що вихідні дані задачі суперечать геометричним властивостям прямокутника, можливо, через помилку або невірно надані вхідні значення. Перевірте дані і впевніться, що вони вірні.