Question

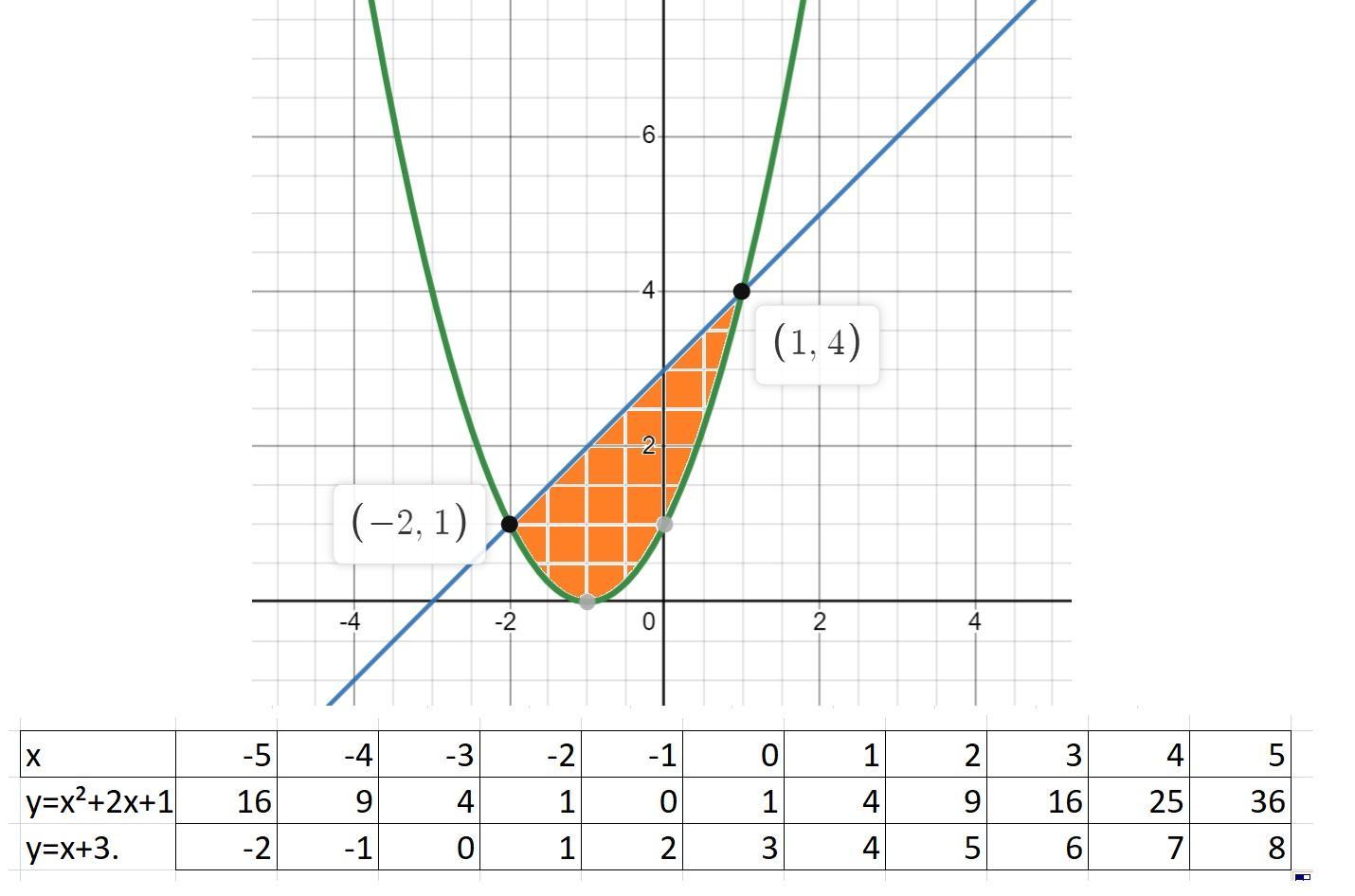
Знайти площу фігури обмеженої лініями y=x²+2x+1 та y=x+3. Зробіть малюнок.

Answer 1

Ответ:    4,5 кв. ед.

Пошаговое объяснение:

Знайти площу фігури обмеженої лініями

1.  Строим графики функций

y=x²+2x+1;

 y=x+3.

2.  Площадь  S=∫(a;b)(f1(x) - f2(x)dx),  где

Пределы интегрирования находим решив систему уравнений

y=x²+2x+1;  y=x+3.=>  x²+2x+1 = x+3;

x²+x-2 = 0;

по т. Виета

x1+x2 = -1;

x1*x2 = -2,

x1=a=-2;

x2 =b= 1.   (См. скриншот)

---------------

f1(x) = (x+3);

f2(x) = x²+2x+1.  Тогда

S=∫(-2;1)((x+3) - (x²+2x+1))dx = ∫(-2;1)(x+3-x²-2x-1)dx =  ∫(-2;1)(-x²-x+2)dx =

=  ∫(-2;1) (-x²)dx - ∫(-2;1)xdx + ∫(-2;1)2dx = -1/3x³|(-2;1) - 1/2x²|(-2;1) + 2x|(-2;1) =

= -1/3(1³-(-2)³) - 1/2(1²-(-2)²) - 2(1-(-2)) = -1/3(1+8) - 1/2(1-4) + 2*3 =

= -9/3+3/2+6 = -3+3/2+6 = 4,5 кв. ед.