Условие задания: 4 Б.
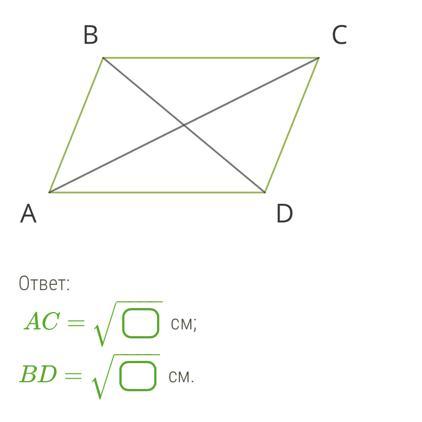
Стороны параллелограмма равны 7 см и 10 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?
э_4.png
Ответ:
AC= −−−−√ см;
BD= −−−−√ см.
Ответить!
Ответы
Ответ:
Для решения этой задачи используем законы косинусов для параллелограмма.
В параллелограмме соседние стороны идентичны и образуют угол \(120^\circ\). Пусть \(a = 7\) см и \(b = 10\) см - стороны параллелограмма, \(c\) - диагональ параллелограмма, а \(\alpha = 120^\circ\) - угол между сторонами.
Закон косинусов гласит:
\[ c^2 = a^2 + b^2 - 2ab \cdot \cos(\alpha) \]
Подставим значения:
\[ c^2 = 7^2 + 10^2 - 2 \cdot 7 \cdot 10 \cdot \cos(120^\circ) \]
Вычислим косинус \(120^\circ\):
\[ \cos(120^\circ) = -\frac{1}{2} \]
Теперь подставим это значение:
\[ c^2 = 49 + 100 + 70 = 219 \]
Таким образом, диагональ параллелограмма \(c\) равна корню из 219:
\[ c = \sqrt{219} \, \text{см} \]
Ответ:
\[ AC = BD = \sqrt{219} \, \text{см} \]
Объяснение:
ввв
Условие задания: 4 Б.
Стороны параллелограмма равны 7 см и 10 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?
э_4.png
Ответ:
AC= −−−−√ см;
BD= −−−−√ см.
Ответить!
Условие задания: 4 Б. Стороны параллелограмма равны 7 см и - 1
Спросите goncharenkololpi29 о заданном вопросе...
goncharenkololpi29 ждет твою помощь.
Ответь и заработай баллы.
Ответ
Никто ещё не оценил этот ответ — почему бы не стать первым?
author link
mosayjenkodn
хорошист
29 ответов
61 пользователей, получивших помощь
Ответ:
Для решения этой задачи используем законы косинусов для параллелограмма.
В параллелограмме соседние стороны идентичны и образуют угол \(120^\circ\). Пусть \(a = 7\) см и \(b = 10\) см - стороны параллелограмма, \(c\) - диагональ параллелограмма, а \(\alpha = 120^\circ\) - угол между сторонами.
Закон косинусов гласит:
\[ c^2 = a^2 + b^2 - 2ab \cdot \cos(\alpha) \]
Подставим значения:
\[ c^2 = 7^2 + 10^2 - 2 \cdot 7 \cdot 10 \cdot \cos(120^\circ) \]
Вычислим косинус \(120^\circ\):
\[ \cos(120^\circ) = -\frac{1}{2} \]
Теперь подставим это значение:
\[ c^2 = 49 + 100 + 70 = 219 \]
Таким образом, диагональ параллелограмма \(c\) равна корню из 219:
\[ c = \sqrt{219} \, \text{см} \]
Ответ:
\[ AC = BD = \sqrt{219} \, \text{см} \]
Объяснение: