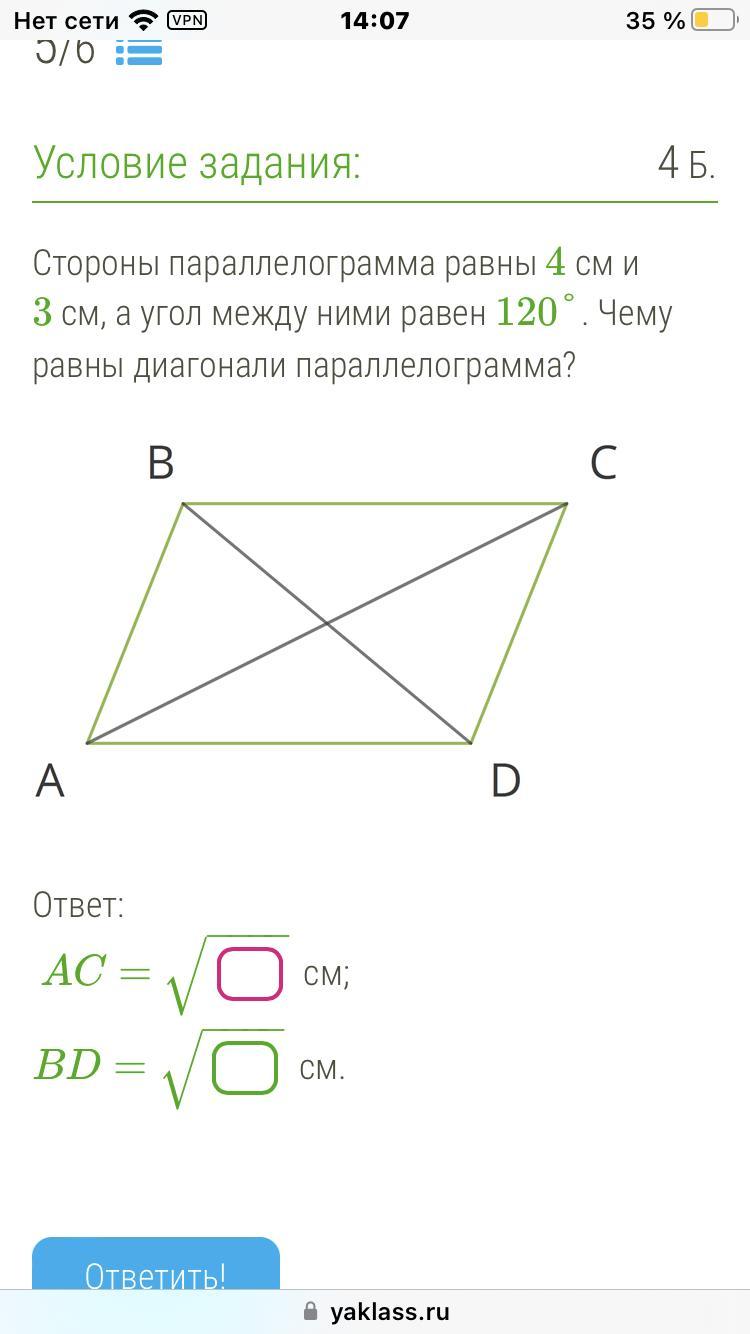
Стороны параллелограмма равны 4 см и 3 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?
Ответы
Ответ:
Для нахождения диагоналей параллелограмма можно воспользоваться законами косинусов.
В параллелограмме соседние стороны идентичны, образуя угол \(120^\circ\). Пусть \(a = 4\) см и \(b = 3\) см - стороны параллелограмма, \(c_1\) и \(c_2\) - диагонали параллелограмма, а \(\alpha = 120^\circ\) - угол между сторонами.
Закон косинусов гласит:
\[ c^2 = a^2 + b^2 - 2ab \cdot \cos(\alpha) \]
Для обеих диагоналей \(c_1\) и \(c_2\) формула одинакова:
\[ c^2 = 4^2 + 3^2 - 2 \cdot 4 \cdot 3 \cdot \cos(120^\circ) \]
Вычислим косинус \(120^\circ\):
\[ \cos(120^\circ) = -\frac{1}{2} \]
Теперь подставим это значение:
\[ c^2 = 16 + 9 + 12 = 37 \]
Таким образом, диагонали параллелограмма \(c_1\) и \(c_2\) равны корню из 37:
\[ c_1 = c_2 = \sqrt{37} \, \text{см} \]
Объяснение:
ч