Предмет: Геометрия,
автор: Аноним
Условие задания: 4 Б.
Стороны параллелограмма равны 7 см и 10 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?
э_4.png
Ответ:
AC= −−−−√ см;
BD= −−−−√ см.
Ответить!
Ответы
Автор ответа:
1
Ответ:
Угол между сторонами параллелограмма равен 120° . Значит второй угол, прилежащий стороне параллелограмма, равен 60° .
Диагонали параллелограмма найдём по теореме косинусов .
Приложения:
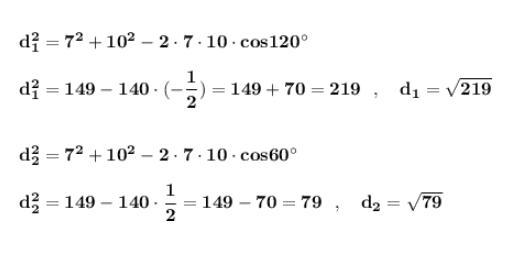
NNNLLL54:
:)
Похожие вопросы
Предмет: Другие предметы,
автор: krivolapalena926
Предмет: Химия,
автор: nixar99
Предмет: Українська мова,
автор: crazydonaterggyt
Предмет: Українська мова,
автор: maryhavrykova099
Предмет: Английский язык,
автор: adlannurudinov96