Предмет: Алгебра,
автор: hamuuuuuud
можете написать решение желательно на листочке пожалуйста
Приложения:
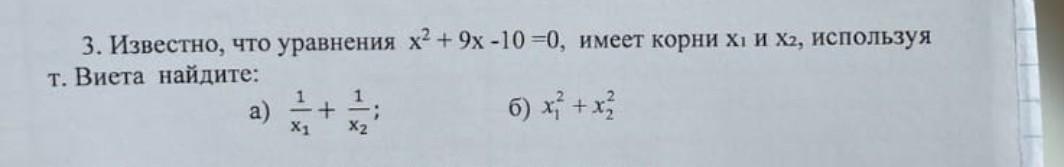
Ответы
Автор ответа:
0
Ответ:
По теореме Виета имеем :
Найдём значения выражений :
Приложения:
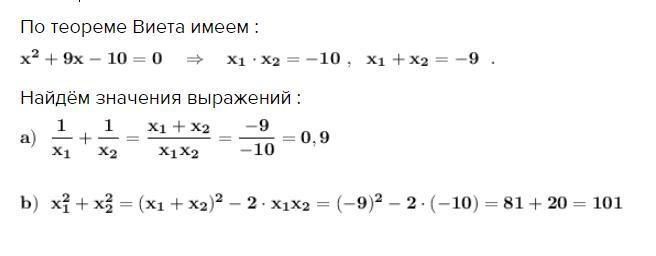
hamuuuuuud:
точно правильно?
Естественно, правильно . Ведь можно проверить . По т.Виета корни равны х1= -10 , х2=1 . 1./10 + 1/1 = 1 - 0,1 = 0,9 ; (-10)^2 + 1^2 = 100 +1 = 101 .
Похожие вопросы
Предмет: Українська мова,
автор: lerastadnik87938
Предмет: Астрономия,
автор: Tyankanax
Предмет: Алгебра,
автор: Dudossa
Предмет: Алгебра,
автор: dasanovickaa7
Предмет: Қазақ тiлi,
автор: nafisa190588