....................
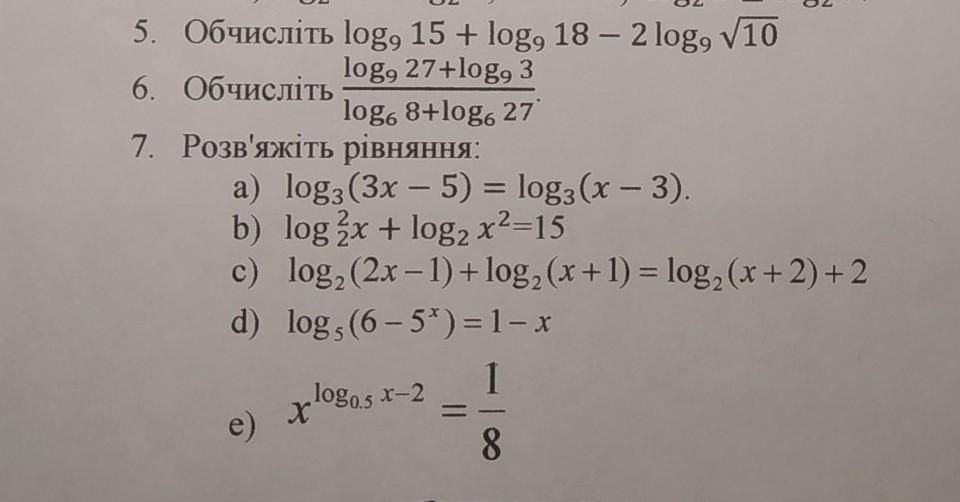
Ответы
Ответ:
1.Объяснение:Обчислимо вираз log9(15) + log9(18) - 2 log9(√10):
Згідно з властивостями логарифмів, log9(15) + log9(18) - 2 log9(√10) = log9(15*18) - log9(√10)^2 = log9(270) - log9(10) = log9(27*10) - log9(10) = log9(27) + log9(10) - log9(10) = log9(27).
Отже, значення виразу log9(15) + log9(18) - 2 log9(√10) дорівнює log9(27).
2.Обчислимо вираз log6(27) + log9(3) + log6(8) + log6(27):
Згідно з властивостями логарифмів, log6(27) + log9(3) + log6(8) + log6(27) = log6(27278*3) = log6(17496).
3.Розв'яжемо рівняння: a) log3(3x-5) = log3(x - 3)
Застосуємо властивість логарифмів, яка дозволяє скоротити обидві сторони рівняння, отримаємо: 3x - 5 = x - 3 2x = 2 x = 1
b) log(2x) + log(x^2) = 15
Спочатку об'єднаємо логарифми за допомогою властивості логарифмів: log(2x * x^2) = 15 log(2x^3) = 15
Застосуємо властивість логарифмів, щоб позбутися від логарифму: 2x^3 = 10^15 x^3 = 5^15 x = 5^5
c) log2(2x-1)+log2(x+1)= log2(x+2)+2
Об'єднаємо логарифми за допомогою властивості логарифмів: log2((2x-1)*(x+1))= log2((x+2)*2^2) log2(2x^2+x-1) = log2(4x+8)
Застосуємо властивість логарифмів, щоб позбутися від логарифму: 2x^2+x-1 = 4x+8 2x^2 - 3x - 9 = 0
Застосуємо квадратне рівняння, щоб розв'язати для x.
d) logs (6-5)=1-x
Застосуємо властивість логарифмів, щоб позбутися від логарифму: 6-5 = 10^(1-x) 1 = 10^(1-x)
e) xlog₈(x-2) = 1-x
Застосуємо властивість логарифмів, щоб позбутися від логарифму: x * log₈(x-2) = 1-x