Предмет: Алгебра,
автор: alenadobrova
Решение нужно расписать, просто ответ не подходит!!
Приложения:
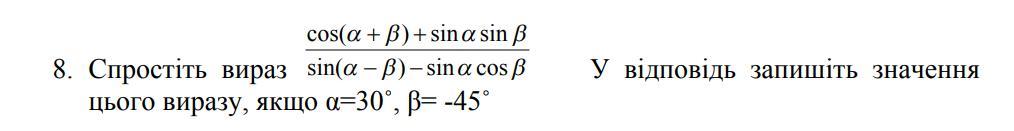
Ответы
Автор ответа:
3
Ответ:
Упростим выражение . Применим формулы косинуса суммы и синуса разности .
Вычислим значение выражения при .
Возможно, если результат не сходится с ответом , то в условие вкралась описка , и оно было таким :
Приложения:


kimkarina953:
Здравствуйте, не могли бы помочь с алгеброй пожалуйста
Похожие вопросы
Предмет: География,
автор: rsapoval09
Предмет: Другие предметы,
автор: mykolaleskov2011
Предмет: География,
автор: alonakvasha9
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: armenmelkonan367