Предмет: Геометрия,
автор: zwuqss
помогите пожалуйста, очень срочно!!
Приложения:
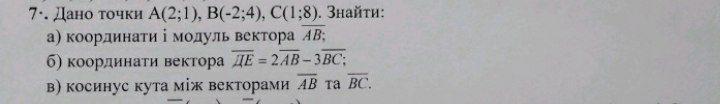
Ответы
Автор ответа:
1
Дано точки А(2;1), В(-2;4), С(1:8). Найти:
а) координати і модуль вектора АВ: б) координати вектора
ДЕ = 2АВ-3BC; в) косинус кута між векторами АВ та ВС.
Объяснение:
А) Координаты вектора (-2-1;4-1) или
(-4;3).
б)Координаты вектора (3;4).
Ищем кординаты вектора ДЕ
х(ДЕ)=2*х(АВ)-3*х(ВС) или х(ДЕ)=2*(-4)-3*3=-8-9=-17,
у(ДЕ)=2*у(АВ)-3*у(ВС) или у(ДЕ)=2*3-3*4=6-12=-6.
Кординаты вектора ДЕ(-17;-6).
в)Найдем косинус угла между векторами через скалярное произведение векторов *
=|AB|*|BC|*cos(AB,DC).
*
=-4*3+3*4=0. Длины можно не искать ( не пригодятся).
|AB|=√((-4)²+3²)=5,
|BC|=√(3²+4²)=5.
cos(AB,DC)=
orjabinina:
Пункт в) поменяла
у меня в профиле есть ещё два вопроса по 100 баллов, можешь помочь пж
Похожие вопросы
Предмет: Биология,
автор: Annuhca779
Предмет: Алгебра,
автор: d7886215
Предмет: Литература,
автор: Njaa
Предмет: Қазақ тiлi,
автор: orakbaigulsaya09
Предмет: Другие предметы,
автор: olgo88