Предмет: Геометрия,
автор: fanatmizuki
Синус острого угла равнобедренной трапеции равен √3/2, боковая сторона — 8дм, а малое основание — 6,4дм. Найдите высоту трапеции и большое основание.
Ответы
Автор ответа:
1
Дано:
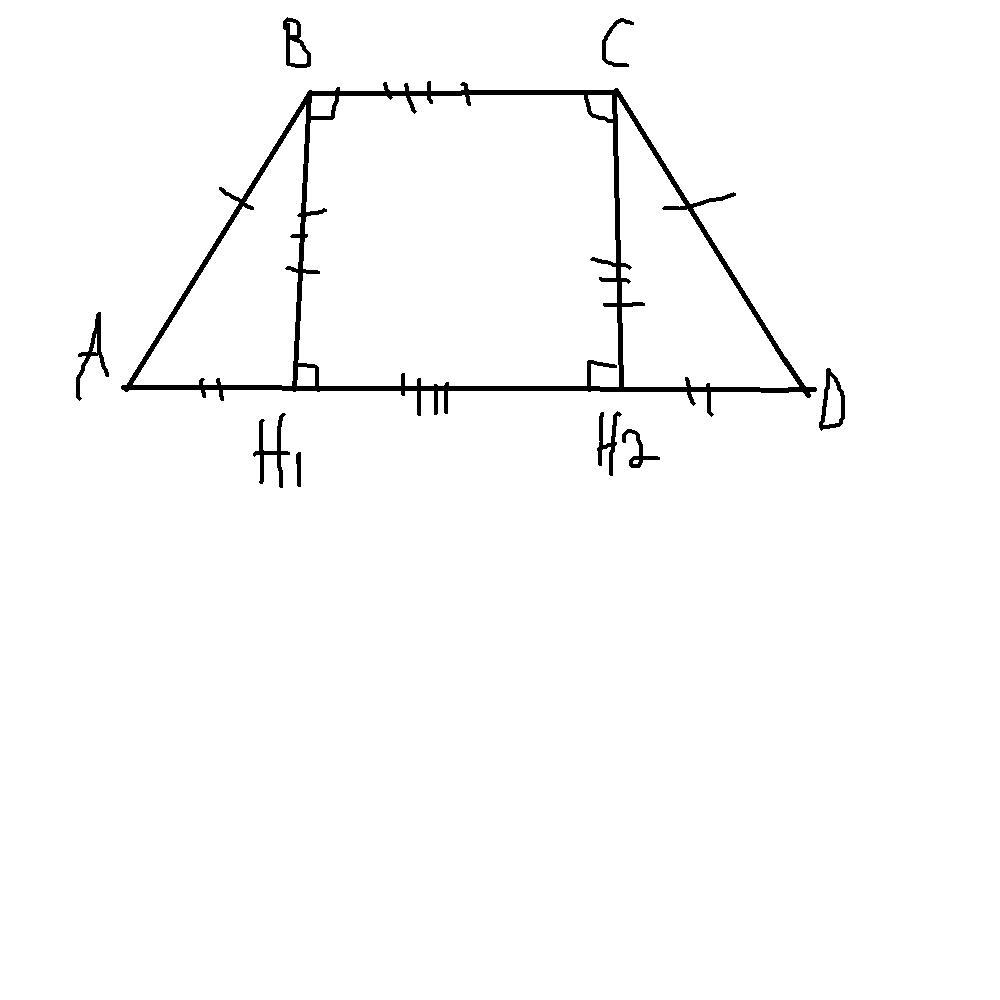
ABCD - равнобедренная трапеция,
BH₁ - высота,
AB = CD = 8 дм, BC = 6,4 дм,
sin∠A = .
Найти:
AD, BH₁
Решение:
Рассмотрим Δ ABH₁ - прямоугольный, ∠AH₁B = 90°, тогда
По т. синусов,
.
По т. Пифагора,
Проведем высоту CH2,
AH1 = H2D = 4 дм.
Рассмотрим прямоугольник BH1CH2,
BC = H1H2 = 6,4 дм,
BH1 = CH2 = дм, тогда
AD = AH1 + H1H2 + H2D = 4 + 6,4 + 4 = 14,4 дм.
Ответ, AD = 14,4 дм, BH1 = дм.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: lisa1377
Предмет: Українська мова,
автор: orisagerus8
Предмет: Українська мова,
автор: anamakarcuk4
Предмет: Русский язык,
автор: gvbcifju
Предмет: Русский язык,
автор: hokagedaniar