Question

Р – внутрішня точка правильного трикутника АВС, така, що AP²=BP²+ CP² Знайти кут ВРС.

Answer 1

Ответ:

Угол ВРС равен 150°.

Объяснение:

Р-внутренняя точка правильного треугольника АВС, такая, что AP²=BP² + CP². Найти угол ВРС.

Дано: ΔАВС - равносторонний;

Р ∈ (АВС)

AP²=BP² + CP²

Найти: ∠ВРС

Решение:

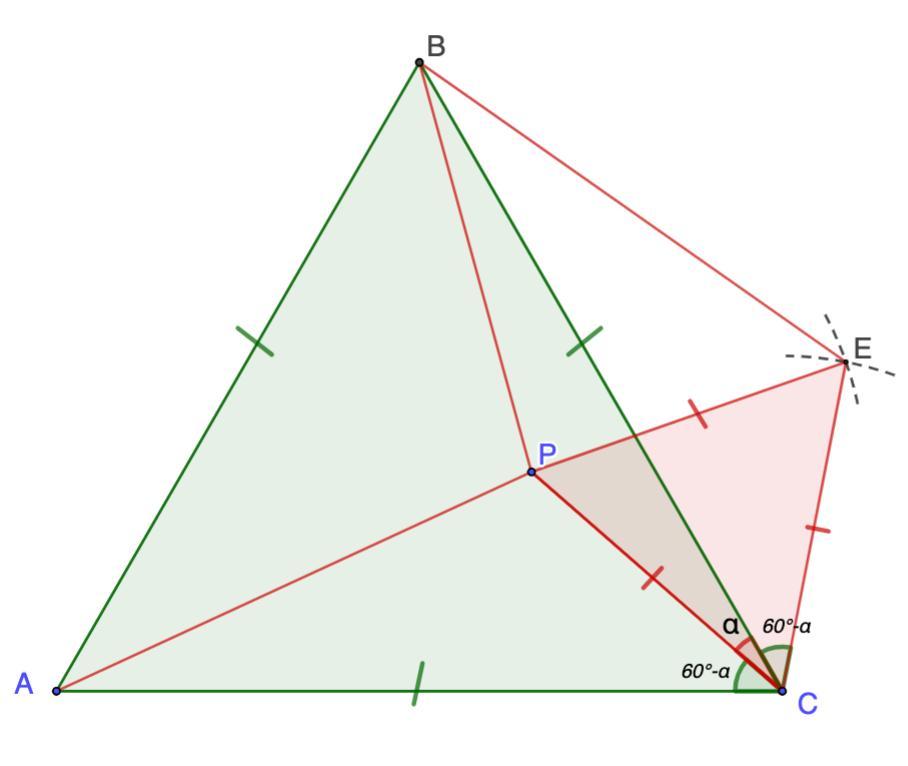
Дополнительное построение:

на отрезке РС построим равносторонний ΔРСЕ. Соединим Е и В.

• В равностороннем треугольнике углы равны 60°.

Пусть ∠РСВ = α   ⇒   ∠АСР = 60° - α, ∠ВСЕ = 60° - α

Рассмотрим ΔАРС и ΔВЕС.

∠АСР = ∠ВСЕ = 60° - α

АС = ВС (условие); РС = ЕС (построение)

⇒ ΔАРС = ΔВЕС (по 1 признаку)

⇒ АР = ВЕ (как соответственные элементы)

AP² = BP² + CP² (условие)

Рассмотрим ΔРВЕ

АР = ВЕ (см. выше); СР = РЕ (построение)

⇒  ВЕ² = ВР² + РЕ²   ⇒   ΔРВЕ - прямоугольный.

∠ВРС = ∠ВРЕ + ∠СРЕ = 90° + 60° = 150°

#SPJ1